reveal.js

# Procedures

---

CS 130 // 2021-10-11

## Administrivia
- Quiz 2 debrief
- 
 Quiz 3 on Wednesday
    + Translating some simple C to MIPS like we've been doing this last week

# Questions
## ...about anything?

# Conditionals

## Conditionals

- `beq` `$s0`, `$s1`, `label`
    + 
 "Branch when equal"
    + 
 If `$s0` is equal to `$s1`, then jump to `label`
- 
 `bne` `$s0`, `$s1`, `label`
    + 
 "Branch when not equal"
    + 
 If `$s0` does not equal `$s1`, then jump to `label`
- 
 `slt` `$t0`, `$s0`, `$s1` (`slti` variant)
    + 
 "Set on less than"
    + 
 `$t0` = 1 if `$s0` < `$s1` else 0

## Compiling an `if` Statement

```c
if (i == j)   // $s0 <- i,  $s1 <- j
    k = 1;    // $s2 <- k

m = 0;        // $s3 <- m
```

---

```mips
      bne $s0, $s1, Exit
      li  $s2, 1
Exit: li  $s3, 0
```

```c
if (i == j)   // $s0 <- i,  $s1 <- j
    k = 1;    // $s2 <- k
else 
    k = 2;

m = 0;        // $s3 <- m
```

---

```mips
      bne  $s0, $s1, Else
      li $s2, 1
      j Exit
Else: li $s2, 2
Exit: li $s3, 0
```

```c
if (i == j)   // $s0 <- i,  $s1 <- j
    k = 1;    // $s2 <- k
else if (i != g)
    k = 2;
else
    k = 3;

m = 0;       // $s3 <- m
```

---

```mips
        bne $s0, $s1, ElseIf
        li  $s2, 1
        j   Exit

ElseIf: beq $s0, $s3, Else
        li  $s2, 2
        j   Exit

Else:   li  $s2, 3
Exit:   li  $s3, 0
```

## Compiling a `while` Statement

```c
while (i != 10)   // $s0 <- i
{
    i++;
}
j = 0;            // $s1 <- j
```

---

```mips
      li   $t0, 10
Loop: beq  $s0, $t0, Done
      addi $s0, $s0, 1
      j    Loop
Done: li   $s1, 0
```

# Procedures

### Compile a Simple Leaf Procedure

```c
int func(int x, int y)
{
    return x + y;
}
```

---

```mips
func: add $v0, $a0, $a1
      jr  $ra
```

### Calling Our Leaf Procedure

```c
int func(int x, int y)
{
    return x + y;
}

int main()
{
    func(1, 2);
}
```

---

```mips
func:
    add $v0, $a0, $a1
    jr $ra

main:
    li  $a0, 1
    li  $a1, 2
    jal func
```

### Nested Procedure Calls

```c
int main()
{
    func(1, func(2, func(3, 4)));
}
```

---

```mips
main:
    li  $a0, 3
    li  $a1, 4
    jal func

li   $a0, 2
    move $a1, $v0
    jal  func

li   $a0, 1
    move $a1, $v0
    jal  func
```

## Calling a Procedure
1. Put parameters in appropriate registers
    + 
 `$a0`, `$a1`, `$a2`, `$a3`
2. 
 Transfer control to the procedure
    + 
 `jal ProcedureLabel`
3. 
 Perform task
4. 
 Place result in a location the callee can find
    + 
 `$v0`, `$v1`
5. 
 Return control to the caller
    + 
 `jr $ra`

## Non-Leaf Procedures
- Life would be easy if all procedures were "leaves"
- In reality, a procedure might call another procedure which may call another procedure ...
- 
 We need a way to preserve the state of each partially completed call so that they all return properly

## Non-Leaf Procedures
- The most extreme case of this is **recursion** where the number of calls could be arbitrarily large
    <pre><code class="c" data-trim>
        int termial(int n)
        {
            if (n == 0)
                return 0;
            else
                return n + termial(n - 1);
        }
    </code></pre>
- 
 Before a procedure calls another procedure, it needs to **save** any data that might be overwritten by the procedure call **in memory**

# Stack

## Stack
- MIPS provides a register `$sp` that stores a memory address
- 
 Addresses **above** `$sp` is memory that is already being used by other parts of the program
- 
 Addresses **below** `$sp` is free memory

## Stack
- The **called** procedure is responsible for restoring any saved registers `$s0`, ..., `$s7` as well as the stack pointer `$sp` register before returning
- 
 Any other register may be used without restoration, so the **calling** procedure is responsible for saving any data before making the call

## Memory Structure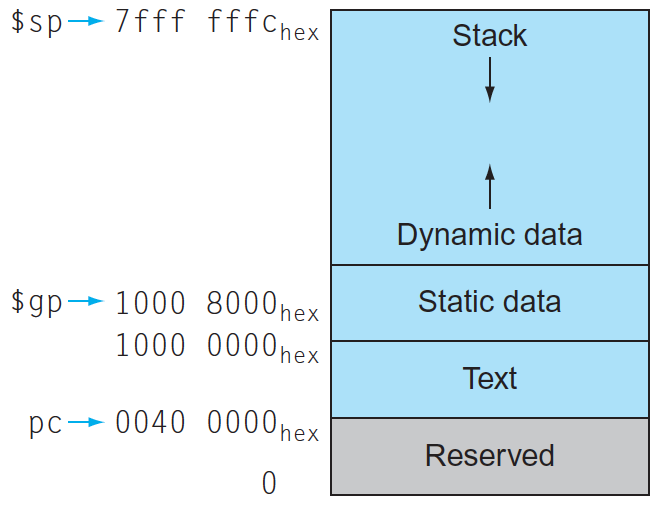
![MIPS memory structure](/teaching/2021f/cs130/assets/images/COD/mips-memory.png)

## Stack Frames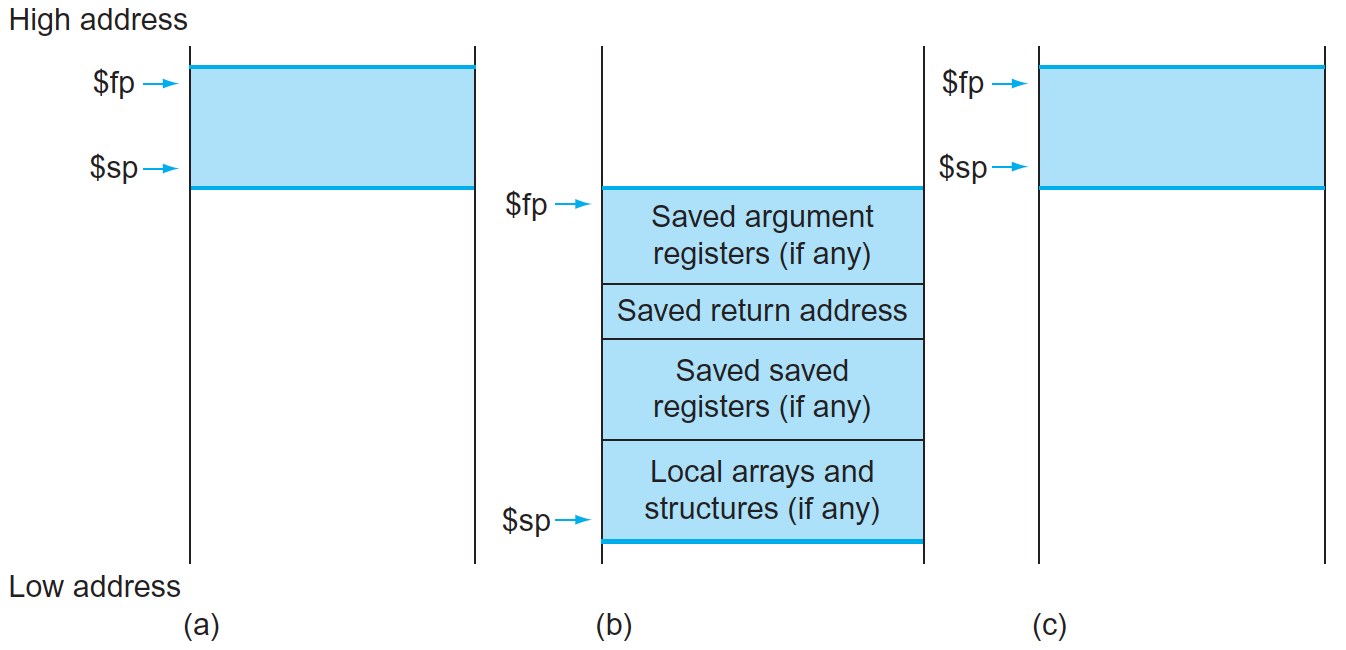
![Procedure frame](/teaching/2021f/cs130/assets/images/COD/stack-frame.png)

## Termial Example
```c
int termial(int n)
{
    if (n == 0)
        return 0;
    else
        return n + termial(n - 1);
}
```

## Termial Example

```mips
termial:  beq  $a0, $zero, ret_zero   # Checks base case
          addi $sp, $sp, -8           # Allocates space
          sw   $ra, 0($sp)            #   for $ra and n
          sw   $a0, 4($sp)            #   on the stack
          addi $a0, $a0, -1           # Loads n-1 as arg
          jal  termial                # Calls termial(n-1)
          lw   $a0, 4($sp)            # Restores n
          add  $v0, $v0, $a0          # Adds n to result
          lw   $ra, 0($sp)            # Restores $ra
          addi $sp, $sp, 8            # Deallocates memory
          jr   $ra                    # Returns result

ret_zero: li   $v0, 0                 # Returns 0
          jr   $ra
```

## Exercise
- Convert the following C code into MIPS

```c
int compute (int e)
{
    return e + e;
}
int calc(int c)
{
    int d = compute(7);
    return c + d;
}
int main()
{
    int a = 5;
    int b = calc(a);
}
```

## Exercise: Compute

```c
int compute (int e)
{
    return e + e;
}
```

```mips
compute: add $v0, $a0, $a0    # returns e + e
         jr $ra
```

## Exercise: Calc - Take 1

```c
int calc(int c)
{
    int d = compute(7);
    return c + d;
}
```

```mips
calc: li  $a0, 7          # puts 7 in a0
      jal compute         # calls compute(7)
      add $v0, $v0, $a0   # adds argument to result
      jr  $ra
```

- 
 Unfortunately this will fail. Why?
    + 
 Both `$a0` and `$ra` will be erased!

## Exercise: Calc - Take 1

```c
int calc(int c)
{
    int d = compute(7);
    return c + d;
}
```

```mips
calc: addi $sp, $sp, -8    # allocates space
      sw   $a0, 0($sp)     # stores c on the stack
      sw   $ra, 4($sp)     # stores $ra on the stack
      li   $a0, 7          # puts 7 in a0
      jal  compute         # calls compute(7)
      lw   $ra, 4($sp)     # restores $ra
      lw   $a0, 0($sp)     # restores argument
      addi $sp, $sp, 8     # deallocates space
      add  $v0, $v0, $a0   # adds argument to result
      jr   $ra
```

## Exercise: Main

```c
int main()
{
    int a = 5;
    int b = calc(a);
}
```

```mips
main:    li   $s0, 5          # a = 5
         move $a0, $s0        # loads a into argument
         jal  calc            # calls calc(5)
         move $s1, $v0        # b = result
```

# Tail Recursion

## Tail Calls
- A **tail call** is when a procedure immediately returns the result of another procedure
    ```c
    int foo(int x)
    {
        return x + x;
    }

int bar(int x)
    {
        int y = x + x;
        return foo(y);
    }
    ```
- 
 A tail call can be implemented **without** creating a new procedure frame

## Tail Calls

```c
int foo(int x)
{
    return x + x;
}

int bar(int x)
{
    int y = x + x;
    return foo(y);
}
```

```mips
foo: add $v0, $a0, $a0
     jr  $ra

bar: add $a0, $a0, $a0
     j   foo
```

## Tail Recursion
- If a function makes tail calls to itself, it is called **tail recursive**
- 
 Is our implementation of `termial` tail recursive?
    ```c
    int termial(int n)
    {
        if (n == 0)
            return 0;
        else
            return n + termial(n - 1);
    }
    ```
- 
 No! It has to add `n` before returning

## Tail Recursion
- Can we implement it tail recursively?

```c
int terminal(int n) {
    return termial_helper(n, 0);
}

int termial_helper(int n, int so_far) {
    if (n == 0)
        return 0;
    else
        return termial_helper(n - 1, n + so_far);
}
```

## Tail Recursion
- What does this look like in MIPS?

```mips
termial:        li $a1, 0
termial_helper: beq $a0, $zero, ret_so_far
                add $a1, $a1, $a0
                j termial_helper
ret_so_far:     move $v0, $a1
                jr $ra
```