reveal.js

# Algorithm Analysis

---

CS 137 // 2021-08-30

# Welcome!
My name is Titus Klinge<br>
(Please call me **Titus**)

---

**Office:** 305 Collier-Scripps<br>
**Email:** <titus.klinge@drake.edu><br>
**Phone:** (515) 271-4599

</div>
<div>

**Office Hours:**<br>
**Tu/Th:** 2:30–4:30 PM<br>
(Held via Zoom)

</div>
</div>

# Introductions

1. 
 I will **badly mispronounce** your name
2. 
 Please stand up and correct my terrible pronunciation
3. 
 Let us know what you preferred to be called
4. 
 Share one hobby or interest you have

# Course Overview

## Themes of the Course
1. Identifying and solving problems **efficiently**
2. 
 Be as **lazy** as possible
    - 
 i.e., **Reduce** problems to well-known related problems rather than solve them from scratch

---

- 
 We want to recognize problems, get to the underlying difficulty behind them, and know what algorithm techniques to apply

## Major Algorithm Design Techniques
1. Divide and Conquer
2. Backtracking
3. Greedy
4. Dynamic Programming

## Algorithm Design
- An algorithm solves a **general problem**
- 
 To specify an algorithmic problem we must define:
    1. 
 The set of **instances** the algorithm works on
    2. 
 The desired properties of the output

## Example Problem: Sorting

- **INPUT:** A sequence of numbers $(a_1,a_2,\ldots a_n)$
- **OUTPUT:** a permutation of the input sequence $(b_1,b_2,\ldots b_n)$ that satisfies $b_1 \le b_2 \le \cdots \le b_n$

---

- 
 We want *correct* and *efficient* algorithms
- 
 A faster algorithm on a slower computer will **always** win for sufficiently large instances

## Specifying an Algorithm
- How can we specify an algorithm?

## Option 1: Actual Code

```py
def insertion_sort(t):
    for i in range(1, len(t)):
        insert_left(t, i)

def insert_left(t, i):
    if i > 0 and t[i] < t[i-1]:
        t[i], t[i-1] = t[i-1], t[i]
        insert_left(lst, i-1)

```

## Option 2: English
- Keep two lists of numbers---one sorted and one unsorted
- Start the unsorted list with one number and the unsorted list with the rest of the numbers
- Take one number from the unsorted list and "insert" it into the sorted list, maintaining its sortedness
- Repeat the above step until the unsorted list is empty---the output is the sorted list

## Option 3: Pseudocode
- Given input $A[n]$, an array of $n$ values, do:
    + For each $i$ from $1$ to $n-1$, do:
        * Set $j = i$
        * While $j > 0$ and $A[j] < A[j-1]$, do:
            - Swap the values of $A[j]$ and $A[j-1]$
        * Set $j = j - 1$

## Specifying Algorithms
- In this course, we will use a combination of real code, pseudocode, and English
- 
 By default, write your solutions in pseudocode, unless I explicitly ask you to "describe" an algorithm or use a specific language

## Correctness
- How do we know when an algorithm is *correct*?
- 
 Sometimes correctness is not obvious at all!

## Example: UPS Routing
- Suppose you work for UPS and are helping route deliveries
- 
 Given a set of delivery locations, we wish to generate a path that visits each location using minimal travel time
- 
 We seek the "shortest tour" of all of the points

## Example: UPS Routing
- **INPUT:** A set of points $\{(x_1,y_1),\ldots (x_n,y_n)\}$
- **OUTPUT:** A path that visits every point exactly once with minimal length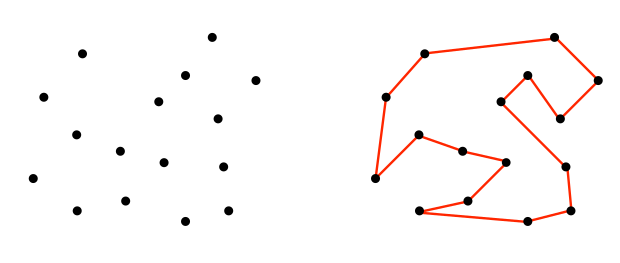

![Set of points with path](/teaching/2021f/cs137/assets/images/robot-tour-points.png)

## Nearest Neighbor Tour
- 
 Given a set of points $S$
    + Pick and visit some initial point $p_0\in S$
    + Let $i = 0$
    + While there are still unvisited points in $S$:
        * Let $p_{i+1}$ be the closest unvisted point to $p_i$
        * Visit $p_{i+1}$
        * Let $i = i + 1$
    + Return the path $(p_0, p_1, \ldots, p_{n-1})$

## Nearest Neighbor is Wrong!
- 
 Consider the following set of points where $p_0 = 0$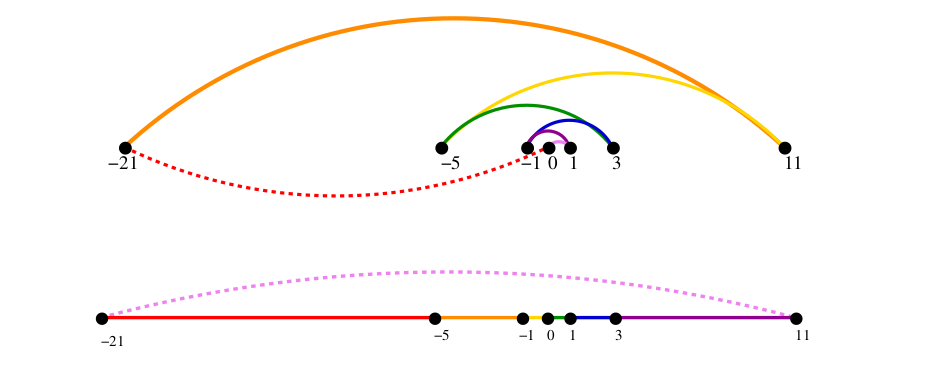 
  ![Nearest neighbor counterexample](/teaching/2021f/cs137/assets/images/nearest-neighbor-counterexample.png)
- 
 Starting from the left doesn't fix the problem!

## Proving Correctness
- Must **prove** that an algorithm always returns the desired output for all legal instances of the problem

## Exhaustive Search
- Consider the algorithm of trying all possible orderings of points and returning the shortest

---

- 
 Given a set of points $S$
    + Let $d = \infty$
    + For each permutation, $\pi$, of the points $S$:
        * If $\text{cost}(\pi) < d$ then:
            - $d = \text{cost}(\pi)$ and $\pi_\text{min} = \pi$
    + Return $\pi_\text{min}$

## Exhaustive Search
- Since all possible paths are considered, this approach will always return the shortest tour
- 
 How many total paths are there?
    + 
 $n!$ permutations!
    + 
 This algorithm is so slow that it useless for more than a dozen or two points
- 
 Later we will see that **no** efficient algorithm exists to solve the traveling salesman problem

## Types of Proofs
- Proofs often fall into these categories:
    + 
 Direct Proof
    + 
 Proof by Construction / Counterexample
    + 
 Proof by Contradiction
    + 
 Proof by Induction

# Course Logistics

## Course Website

[analytics.drake.edu/teaching/2021f/cs137](https://titusklinge.com/teaching/2021f/cs137/)

# Assignment 1
Due **Wednesday, September 1st** (before class)

1. Read the **syllabus**
2. Complete a **questionnaire**
3. Start the assigned **readings**
4. Do the first daily exercise