reveal.js

# Asymptotic Notation, Continued

---

CS 137 // 2021-09-08

## Administrivia
- You should have turned in:
    + Your reflection for daily exercise 1
    + Your solution to daily exercise 2
- 
 Returned assignment 1 on Gradescope
    + Decided **not** to assign seating, but please consider sitting in the same spot for the whole term

## Administrivia
- Textbook clarification:
    + **No textbook** is required for this course
    + We will be using the book provided for free by Cowles library

# Questions
## ...about anything?

# Big Oh Notation

## $f(n) = O(g(n))$
$f$ is "big oh" of $g$

- **Informally:**
    + $g$ is an **upper bound** for $f$
- 
 **Formally:**
    + There is a constant $c>0$ such that $f(n) \le c\cdot g(n)$ for all $n\ge n_0$
</div>
<div>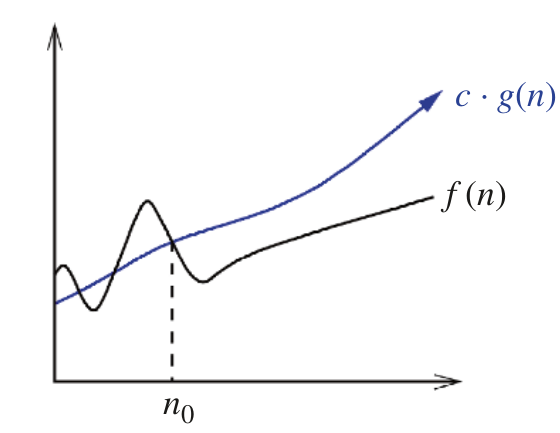

![Big Oh](/teaching/2021f/cs137/assets/images/big-oh.png)

</div>
</div>

## $f(n) = \Omega(g(n))$
$f$ is "big omega" of $g$

- **Informally:**
    + $g$ is an **lower bound** for $f$
- 
 **Formally:**
    + There is a constant $c>0$ such that $f(n) \ge c\cdot g(n)$ for all $n\ge n_0$
</div>
<div>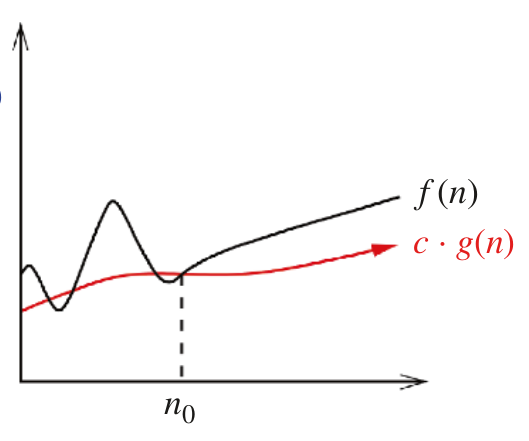

![Big Omega](/teaching/2021f/cs137/assets/images/big-omega.png)

</div>
</div>

## $f(n) = \Theta(g(n))$
$f$ is "big theta" of $g$

- **Informally:**
    + $g$ is a **tight bound** for $f$
- 
 **Formally:**
    + There exist constants $c_1,c_2>0$ such that $c_1g(n) \ge f(n) \ge c_2g(n)$ for all $n\ge n_0$
- 
 **Alternatively:**
    + $f(n) = O(g(n)) = \Omega(g(n))$
</div>
<div>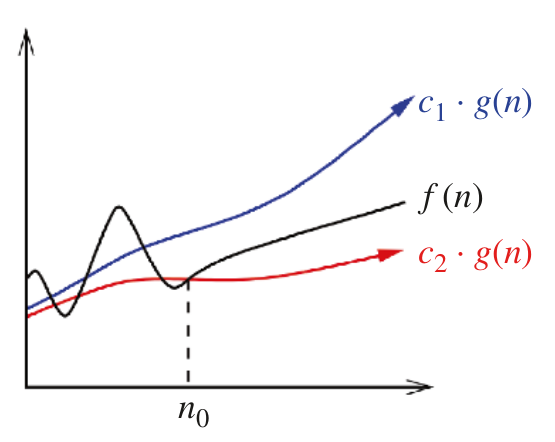

![Big Theta](/teaching/2021f/cs137/assets/images/big-theta.png)

</div>
</div>

# Daily Exercise

## Big Oh Comparison
- In practice, speeding up an algorithm by 2x is great even though $f(n)$ and $f(n)/2$ have the same asymptotic time complexity
- 
 However, a jump from $n^2$ to $n\log n$ is a **CRAZY HUGE IMPROVEMENT**

## Big Oh Comparison

| $n$    || $n^2$   | $n^2/2$ | $n\log n$
|--------||---------|---------|-----------
| $10$   || $100$   | $50$      | $33$
| $100$  || $10000$ | $5000$    | $664$
| $10^3$ || $10^6$  | $5\times 10^5$    | $9965$
| $10^4$ || $10^8$  | $5\times 10^7$    | $1.3\times 10^5$
| $10^5$ || $10^{10}$  | $5\times 10^9$    | $1.6\times 10^6$

# Dominance Relations

## Dominance Relations
- When $f(n) = O(g(n))$ but $f(n) \ne \Theta(g(n))$, we say that $g$ **dominates** $f$
    + 
 Sometimes written $f(n) \ll g(n)$
    + 
 Sometimes written $f(n) = o(g(n))$
    + 
 $f$ is "little oh" of $g$

## Another Characterization
- With functions $f(n)$ and $g(n)$, consider the behavior of the limit:
    $$\lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}$$
- 
 What if it diverges to $\infty$?
- 
 What if it converges to $0$?
- 
 What if it converges to a constant $c > 0$?

## Another Characterization

$$\begin{aligned}
f(n) \gg g(n) &\iff \lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=\infty\\\\
f(n) \ll g(n) &\iff \lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=0\\\\
f(n) = \Theta(g(n)) &\iff \lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=c > 0
\end{aligned}$$

## Applications of Dominance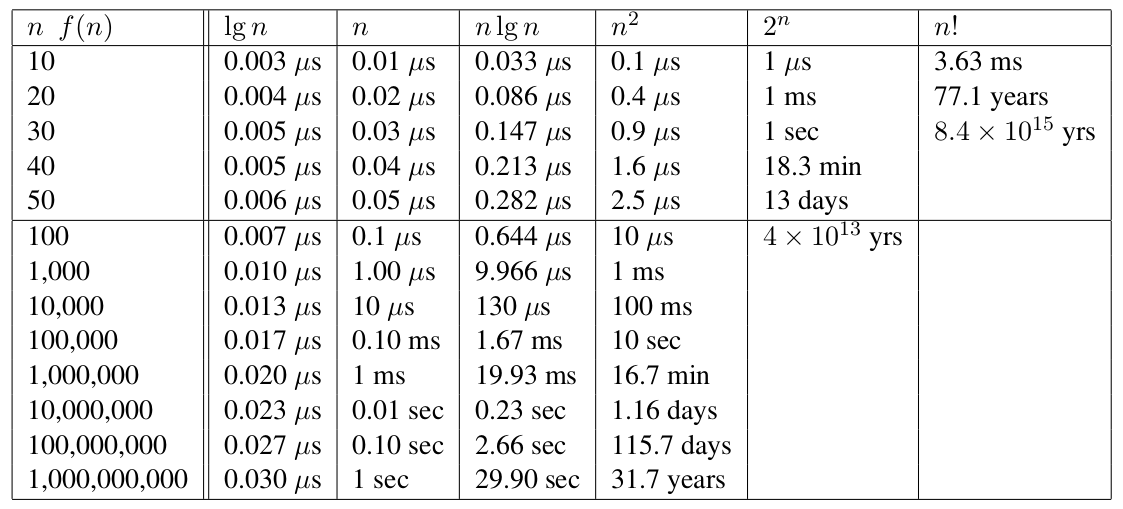

![Dominance Table](/teaching/2021f/cs137/assets/images/dominance.png)

## Applications of Dominance
- Exponential algorithms are hopelessly slow
- 
 Quadratic algorithms get hopeless around $n=1000000$
- 
 $O(n\log n)$ algorithms get hopeless around $n=10^9$
- 
 $O(\log n)$ is extremely fast, even for extraordinary large values of $n$

## Exercises
- Determine whether each of the following statements is true or false:
    + 
 $f(n) = O(g(n))$ is the same as $g(n) = \Omega(f(n))$
    + 
 If $f(n) = O(g(n))$, then $f(n) = o(g(n))$<br>(i.e., $g$ *dominates* $f$)
    + 
 If $f(n) = o(g(n))$, then $f(n) = O(g(n))$

## Exercises
- Consider the following algorithm
    ```java
    public int search(String[] arr, String val) {
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] == val) {
                return i;
            }
        }
        return -1;
    }
    ```
- What is the **worst-case** runtime of `search`?

## Exercises
- Consider this algorithm where `arr` is sorted
    ```java
    public int search(double[] arr, double val) {
        int start = 0;
        int end = arr.length - 1;
        while (start <= end) {
            mid = (start + end) / 2;
            if (arr[mid] == val) {
                return mid;
            } else if (arr[mid] < val) { 
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }
        return -1;
    }
    ```
- What is the **worst-case** runtime of `search`?

- Consider the following algorithm
    ```java
    public void foo(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            bar(arr, arr[i]);
        }
        baz(arr);
    }
    ```
- What is the **worst-case** runtime of `foo` given that:
    + `bar` is $O(1)$ and `baz` is $O(1)$
    + 
 `bar` is $O(n)$ and `baz` is $O(1)$
    + 
 `bar` is $O(1)$ and `baz` is $O(n)$
    + 
 `bar` is $O(n)$ and `baz` is $O(2^n)$

## Reminders
- Do a reflection for DE-2
- Do DE 3 before Monday