reveal.js

# Binary Search Trees

---

CS 137 // 2021-09-15

## Administrivia
- You should have turned in:
    + Your reflection for daily exercise 3
    + Your solution to daily exercise 4

# Questions
## ...about anything?

# Daily Exercise

# Review

##  Sequential Data Structures

| **Operation**   | **Array** | **Linked** |
|-----------------|-----------|------------|
| `add to front`  | O(1)*     | O(1)       |
| `add to back`   | O(1)*     | O(1)       |
| `remove front`  | O(1)      | O(1)       |
| `remove back`   | O(1)      | O(1)       |
| `random access` | O(1)      | O(n)       |

- O(1)* means "amortized" constant time

## Dictionary Data Structure

| **Operation**   | **Unsorted** | **Sorted** |
|-----------------|--------------|------------|
| `search`        | O(n)         | O(log n)   |
| `insert`        | O(1)         | O(n)       |
| `delete`        | O(n)*        | O(n)       |

- Assumes using a sequential container implementation (e.g. array or linked list)
- 
 The O(n)* can be improved to O(1) for deletion if we know the index of the element

# Binary Search Trees

## Review: Linked Lists
- Linked lists consists of a sequence of "nodes"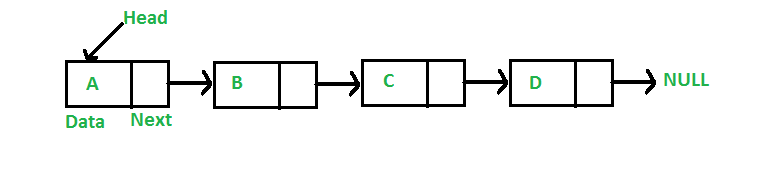
    ![Linked List](https://media.geeksforgeeks.org/wp-content/cdn-uploads/gq/2013/03/Linkedlist.png)
- 
 Nodes contain at least two things:
    1. A **value** that is stored in the node
    2. A **pointer** to the next node in the sequence

## Review: Linked Lists
- An implementation of the `Node` type typically looks something like the following:

```java
class Node<E> {
    E value;    // data stored inside the node
    Node next;  // pointer to the next element
}
```

## Trees
- A **tree** is a linked data structure where each node has a reference to **zero or more** other nodes

</div>

- 
 Trees are **acyclic**, so the arrows only go "top down"

## Trees
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="278pt" height="188pt"
 viewBox="0.00 0.00 278.00 188.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 184)">
<title>dfa</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-184 274,-184 274,4 -4,4"/>

<g id="node1" class="node">
<title>A</title>
<ellipse fill="none" stroke="black" cx="171" cy="-162" rx="27" ry="18"/>
<text text-anchor="middle" x="171" y="-158.3" font-family="Times,serif" font-size="14.00">A</text>
</g>

<g id="node2" class="node">
<title>B</title>
<ellipse fill="none" stroke="black" cx="99" cy="-90" rx="27" ry="18"/>
<text text-anchor="middle" x="99" y="-86.3" font-family="Times,serif" font-size="14.00">B</text>
</g>

<g id="edge1" class="edge">
<title>A->B</title>
<path fill="none" stroke="black" d="M156.43,-146.83C146.25,-136.94 132.48,-123.55 120.97,-112.36"/>
<polygon fill="black" stroke="black" points="123.41,-109.85 113.8,-105.38 118.53,-114.87 123.41,-109.85"/>
</g>

<g id="node3" class="node">
<title>C</title>
<ellipse fill="none" stroke="black" cx="171" cy="-90" rx="27" ry="18"/>
<text text-anchor="middle" x="171" y="-86.3" font-family="Times,serif" font-size="14.00">C</text>
</g>

<g id="edge2" class="edge">
<title>A->C</title>
<path fill="none" stroke="black" d="M171,-143.7C171,-135.98 171,-126.71 171,-118.11"/>
<polygon fill="black" stroke="black" points="174.5,-118.1 171,-108.1 167.5,-118.1 174.5,-118.1"/>
</g>

<g id="node4" class="node">
<title>D</title>
<ellipse fill="none" stroke="black" cx="243" cy="-90" rx="27" ry="18"/>
<text text-anchor="middle" x="243" y="-86.3" font-family="Times,serif" font-size="14.00">D</text>
</g>

<g id="edge3" class="edge">
<title>A->D</title>
<path fill="none" stroke="black" d="M185.57,-146.83C195.75,-136.94 209.52,-123.55 221.03,-112.36"/>
<polygon fill="black" stroke="black" points="223.47,-114.87 228.2,-105.38 218.59,-109.85 223.47,-114.87"/>
</g>

<g id="node6" class="node">
<title>F</title>
<ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">F</text>
</g>

<g id="edge5" class="edge">
<title>B->F</title>
<path fill="none" stroke="black" d="M84.43,-74.83C74.25,-64.94 60.48,-51.55 48.97,-40.36"/>
<polygon fill="black" stroke="black" points="51.41,-37.85 41.8,-33.38 46.53,-42.87 51.41,-37.85"/>
</g>

<g id="node7" class="node">
<title>G</title>
<ellipse fill="none" stroke="black" cx="99" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="99" y="-14.3" font-family="Times,serif" font-size="14.00">G</text>
</g>

<g id="edge6" class="edge">
<title>B->G</title>
<path fill="none" stroke="black" d="M99,-71.7C99,-63.98 99,-54.71 99,-46.11"/>
<polygon fill="black" stroke="black" points="102.5,-46.1 99,-36.1 95.5,-46.1 102.5,-46.1"/>
</g>

<g id="node5" class="node">
<title>E</title>
<ellipse fill="none" stroke="black" cx="171" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="171" y="-14.3" font-family="Times,serif" font-size="14.00">E</text>
</g>

<g id="edge4" class="edge">
<title>C->E</title>
<path fill="none" stroke="black" d="M171,-71.7C171,-63.98 171,-54.71 171,-46.11"/>
<polygon fill="black" stroke="black" points="174.5,-46.1 171,-36.1 167.5,-46.1 174.5,-46.1"/>
</g>
</g>
</svg>

</div>

- The "top" of the tree is called the **root**
- 
 Every node (except the root) has a **parent**
- 
 Nodes with zero children are called **leaves**
- 
 A tree with no nodes is called **empty**

# Examples of Trees

## Thinking Recursively
- A tree is a **recursive** data structure since every tree has one of two forms:
    + 
 The tree could be **empty** (the root is empty)
    + 
 The tree is rooted with a **node** that contains:
        1. A value stored within the node
        2. A list of other trees (its **children**)

## Binary Trees
- A **binary tree** has nodes with at most two children

</div>

## Binary Trees
- The `Node` type for a binary tree would look something like this:
    ```java
    class Node<E> {
        E value;        // data stored in the node
        Node left;      // left subtree
        Node right;     // right subtree
    }
    ```

## Binary Trees
- A **perfect** binary tree is one where all the leaves share the same level

</div>

- 
 The **height** of a tree is the number of nodes in the longest path from the root to some leaf

## Exercise
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="278pt" height="188pt"
 viewBox="0.00 0.00 278.00 188.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 184)">
<title>dfa</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-184 274,-184 274,4 -4,4"/>

<g id="node1" class="node">
<title>A</title>
<ellipse fill="none" stroke="black" cx="135" cy="-162" rx="27" ry="18"/>
<text text-anchor="middle" x="135" y="-158.3" font-family="Times,serif" font-size="14.00">A</text>
</g>

<g id="node2" class="node">
<title>B</title>
<ellipse fill="none" stroke="black" cx="99" cy="-90" rx="27" ry="18"/>
<text text-anchor="middle" x="99" y="-86.3" font-family="Times,serif" font-size="14.00">B</text>
</g>

<g id="edge1" class="edge">
<title>A->B</title>
<path fill="none" stroke="black" d="M126.65,-144.76C122.29,-136.28 116.85,-125.71 111.96,-116.2"/>
<polygon fill="black" stroke="black" points="114.99,-114.44 107.3,-107.15 108.77,-117.64 114.99,-114.44"/>
</g>

<g id="node3" class="node">
<title>C</title>
<ellipse fill="none" stroke="black" cx="171" cy="-90" rx="27" ry="18"/>
<text text-anchor="middle" x="171" y="-86.3" font-family="Times,serif" font-size="14.00">C</text>
</g>

<g id="edge2" class="edge">
<title>A->C</title>
<path fill="none" stroke="black" d="M143.35,-144.76C147.71,-136.28 153.15,-125.71 158.04,-116.2"/>
<polygon fill="black" stroke="black" points="161.23,-117.64 162.7,-107.15 155.01,-114.44 161.23,-117.64"/>
</g>

<g id="node4" class="node">
<title>E</title>
<ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">E</text>
</g>

<g id="edge3" class="edge">
<title>B->E</title>
<path fill="none" stroke="black" d="M84.43,-74.83C74.25,-64.94 60.48,-51.55 48.97,-40.36"/>
<polygon fill="black" stroke="black" points="51.41,-37.85 41.8,-33.38 46.53,-42.87 51.41,-37.85"/>
</g>

<g id="node5" class="node">
<title>F</title>
<ellipse fill="none" stroke="black" cx="99" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="99" y="-14.3" font-family="Times,serif" font-size="14.00">F</text>
</g>

<g id="edge4" class="edge">
<title>B->F</title>
<path fill="none" stroke="black" d="M99,-71.7C99,-63.98 99,-54.71 99,-46.11"/>
<polygon fill="black" stroke="black" points="102.5,-46.1 99,-36.1 95.5,-46.1 102.5,-46.1"/>
</g>

<g id="node6" class="node">
<title>G</title>
<ellipse fill="none" stroke="black" cx="171" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="171" y="-14.3" font-family="Times,serif" font-size="14.00">G</text>
</g>

<g id="edge5" class="edge">
<title>C->G</title>
<path fill="none" stroke="black" d="M171,-71.7C171,-63.98 171,-54.71 171,-46.11"/>
<polygon fill="black" stroke="black" points="174.5,-46.1 171,-36.1 167.5,-46.1 174.5,-46.1"/>
</g>

<g id="node7" class="node">
<title>H</title>
<ellipse fill="none" stroke="black" cx="243" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="243" y="-14.3" font-family="Times,serif" font-size="14.00">H</text>
</g>

<g id="edge6" class="edge">
<title>C->H</title>
<path fill="none" stroke="black" d="M185.57,-74.83C195.75,-64.94 209.52,-51.55 221.03,-40.36"/>
<polygon fill="black" stroke="black" points="223.47,-42.87 228.2,-33.38 218.59,-37.85 223.47,-42.87"/>
</g>
</g>
</svg>

</div>

- How many nodes does a *perfect binary tree* have if its height is $h$?
- 
 We can sum up the nodes in each level...
    + 
 $1 + 2 + 4 + ...$

## Binary Tree Traversals
- How can we iterate over the elements of a tree?
    + 
 Recursively!
- 
 Given a root node, we need to do:
    1. Process the root
    2. 
 Recursively iterate the left subtree
    3. 
 Recursively iterate the right subtree

## In-Order Traversals
- An **in-order** traversal is one that iterates over the left subtree first, then the root, then the right subtree

```java
void iterateInOrder(Node<E> root) {
    if (root != null) {
        iterateInOrder(root.left);
        // do something with root.value here
        iterateInOrder(root.right);
    }
}
```

## Pre-Order Traversals
- A **pre-order** traversal is one that visits the root, then the left subtree, then the right subtree

```java
void iteratePreOrder(Node<E> root) {
    if (root != null) {
        // do something with root.value here
        iteratePreOrder(root.left);
        iteratePreOrder(root.right);
    }
}
```

## Post-Order Traversals
- A **post-order** traversal is one that iterates over the left subtree, then the right subtree, then the root

```java
void iteratePostOrder(Node<E> root) {
    if (root != null) {
        iteratePostOrder(root.left);
        iteratePostOrder(root.right);
        // do something with root.value here
    }
}
```

# Binary Search Trees

## Binary Search Trees
- Store key/value pairs just like a dictionary
- 
 Keys follow the BST property:
    + For each node in the tree:
        * Every key in the left subtree is **less than** the node's key
        * 
 All keys in the right subtree are **greater than** the nodes's key
    + 
 For now, assume no duplicates, but we could allow them in the left subtree

## Binary Search Tree
```java
class Node<K,V> {
    K key;          // key stored in the node
    V value;        // value stored in the node
    Node left;      // left subtree
    Node right;     // right subtree
}
```

## Binary Search Tree
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="344pt" height="188pt"
 viewBox="0.00 0.00 344.49 188.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 184)">
<title>dfa</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-184 340.49,-184 340.49,4 -4,4"/>

<g id="node1" class="node">
<title>4 // A</title>
<ellipse fill="none" stroke="black" cx="168.75" cy="-162" rx="34.39" ry="18"/>
<text text-anchor="middle" x="168.75" y="-158.3" font-family="Times,serif" font-size="14.00">4 // A</text>
</g>

<g id="node2" class="node">
<title>2 // B</title>
<ellipse fill="none" stroke="black" cx="124.75" cy="-90" rx="35.19" ry="18"/>
<text text-anchor="middle" x="124.75" y="-86.3" font-family="Times,serif" font-size="14.00">2 // B</text>
</g>

<g id="edge1" class="edge">
<title>4 // A->2 // B</title>
<path fill="none" stroke="black" d="M158.54,-144.76C153.23,-136.32 146.62,-125.8 140.66,-116.31"/>
<polygon fill="black" stroke="black" points="143.49,-114.24 135.2,-107.63 137.56,-117.96 143.49,-114.24"/>
</g>

<g id="node3" class="node">
<title>6 // C</title>
<ellipse fill="none" stroke="black" cx="212.75" cy="-90" rx="35.19" ry="18"/>
<text text-anchor="middle" x="212.75" y="-86.3" font-family="Times,serif" font-size="14.00">6 // C</text>
</g>

<g id="edge2" class="edge">
<title>4 // A->6 // C</title>
<path fill="none" stroke="black" d="M178.95,-144.76C184.26,-136.32 190.87,-125.8 196.84,-116.31"/>
<polygon fill="black" stroke="black" points="199.93,-117.96 202.29,-107.63 194.01,-114.24 199.93,-117.96"/>
</g>

<g id="node4" class="node">
<title>1 // D</title>
<ellipse fill="none" stroke="black" cx="35.75" cy="-18" rx="36" ry="18"/>
<text text-anchor="middle" x="35.75" y="-14.3" font-family="Times,serif" font-size="14.00">1 // D</text>
</g>

<g id="edge3" class="edge">
<title>2 // B->1 // D</title>
<path fill="none" stroke="black" d="M106.31,-74.5C93.54,-64.45 76.35,-50.93 62.13,-39.75"/>
<polygon fill="black" stroke="black" points="64.19,-36.92 54.16,-33.49 59.86,-42.42 64.19,-36.92"/>
</g>

<g id="node5" class="node">
<title>3 // E</title>
<ellipse fill="none" stroke="black" cx="124.75" cy="-18" rx="35.19" ry="18"/>
<text text-anchor="middle" x="124.75" y="-14.3" font-family="Times,serif" font-size="14.00">3 // E</text>
</g>

<g id="edge4" class="edge">
<title>2 // B->3 // E</title>
<path fill="none" stroke="black" d="M124.75,-71.7C124.75,-63.98 124.75,-54.71 124.75,-46.11"/>
<polygon fill="black" stroke="black" points="128.25,-46.1 124.75,-36.1 121.25,-46.1 128.25,-46.1"/>
</g>

<g id="node6" class="node">
<title>5 // F</title>
<ellipse fill="none" stroke="black" cx="212.75" cy="-18" rx="34.39" ry="18"/>
<text text-anchor="middle" x="212.75" y="-14.3" font-family="Times,serif" font-size="14.00">5 // F</text>
</g>

<g id="edge5" class="edge">
<title>6 // C->5 // F</title>
<path fill="none" stroke="black" d="M212.75,-71.7C212.75,-63.98 212.75,-54.71 212.75,-46.11"/>
<polygon fill="black" stroke="black" points="216.25,-46.1 212.75,-36.1 209.25,-46.1 216.25,-46.1"/>
</g>

<g id="node7" class="node">
<title>7 // G</title>
<ellipse fill="none" stroke="black" cx="300.75" cy="-18" rx="36" ry="18"/>
<text text-anchor="middle" x="300.75" y="-14.3" font-family="Times,serif" font-size="14.00">7 // G</text>
</g>

<g id="edge6" class="edge">
<title>6 // C->7 // G</title>
<path fill="none" stroke="black" d="M230.98,-74.5C243.52,-64.52 260.37,-51.11 274.37,-39.98"/>
<polygon fill="black" stroke="black" points="276.59,-42.69 282.23,-33.73 272.23,-37.21 276.59,-42.69"/>
</g>
</g>
</svg>

</div>

- If I traverse a binary search tree **in-order**, then the keys will come up in ascending order

## Implementing a Dictionary with a BST
- Recall that common dictionary operations include
    + `search(key)`
    + `insert(key, value)`
    + `delete(key)`
- 
 How would we implement these in a BST?

## Searching in a BST
```java
V search(Node<K,V> node, K key) {
    if (node == null)
        return null;
    else if (key == node.key)
        return node.value;
    else if (key < node.key)
        return search(node.left, key);
    else
        return search(node.right, key);
}
```

## Inserting/Deleting in a BST
- Similar to searching
- 
 For inserting, we search for the location the node *should be* and then add a new node there
- 
 For deleting, we search for the node that contains the key and then remove it

## Runtime Complexity of BST
- If we implement a dictionary using a BST, then what is the complexity of each of these operations?
- 
 $O(h)$ where $h$ is the height of the tree
- 
 If a tree has $n$ nodes, what is the height of the tree?
    + 
 In the worst-case, $O(n)$!

## Self-Balancing Trees
- It is possible to implement BSTs that are **self-balancing**, ensuring that  $h = O(\log n)$
- 
 Two approaches are AVL trees and Red-Black trees

## Self-Balancing Trees
- With self-balancing trees, it is possible to implement a dictionary with the following complexity

| **Operation**   | **BST**      |
|-----------------|--------------|
| `search`        | O(log n)     |
| `insert`        | O(log n)     |
| `delete`        | O(log n)     |