reveal.js

# Introduction to Sorting

---

CS 137 // 2021-09-22

## Administrivia
- You should have turned in:
    + Your reflection for daily exercise 5

# Questions
## ...about anything?

# Review

## Dictionary Implementations

| **Op**   | **BST**     | **HT (Exp)** | **HT (Worst)** |
|----------|-------------|--------------|----------------|
| `search` | $O(\log n)$ | $O(1)$       | $O(n)$         |
| `insert` | $O(\log n)$ | $O(1)$       | $O(n)$         |
| `delete` | $O(\log n)$ | $O(1)$       | $O(n)$         |

- 
 Binary search tree must be self-balancing
- 
 Hashtable's expected runtime depends on the **load factor**, but if properly reallocated is $O(1)$ amortized

## Python Dictionary
- Python's built-in `dict` type is a **hashtable**
- Uses **open addressing** to resolve collisions

## Java Dictionaries
- Java has three implementations of a dictionary in `java.util`:
    + `HashMap` and `Hashtable` both use a hashtable as a backend
    + 
 `Hashtable` is thread-safe but `HashMap` is usually preferred in a single-threaded program
    + 
 `TreeMap` uses a self-balancing BST

# Sorting

## Why talk about sorting...again?
1. Computers spend a lot of time sorting, historically 25% on mainframes
2. 
 Sorting is an excellent problem to study in CS since there are many algorithms known
3. 
 Many other algorithms depend on sorting or can be reduced to the sorting problem

## Sorting Algorithms
- What sorting algorithms have you heard of?

## Sorting Algorithms
<iframe width="840" height="473" src="https://www.youtube.com/embed/ZZuD6iUe3Pc" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

## Efficiency of Sorting

- Sorting algorithms usually fall into two complexity classes:
    + $O(n^2)$
    + $O(n\log n)$
- In some special cases, we can improve this to:
    + $O(n)$

</div>
<div>

| $n$    | $n^2$     |  $n\log n$         |
|--------|-----------|--------------------|
| $10$   | $100$     | $33$               |
| $10^2$ | $10^4$    | $664$              |
| $10^3$ | $10^6$    | $9965$             |
| $10^4$ | $10^8$    | $1.3\times 10^5$   |
| $10^5$ | $10^{10}$ | $1.6\times 10^6$   |

</div>
</div>

## Applications of Sorting
- Many important problems can be directly reduced to sorting or rely on sorting in some way

## Element Uniqueness
- Given a list of $n$ elements, determine whether there are any duplicates

## Finding the Mode
- Given a list of $n$ elements, return the element that appears the most frequently

## Convex Hull
- Given $n$ 2D points, what is the polygon of smallest perimeter that contains the points?

![Convex hull](../../assets/images/convex-hull.png)

## Pragmatics of Sorting
- Suppose we'd like to alphabetize a list of names
- 
 Even in this simple case we face some decisions:
    + 
 Is "Klinge" the same as "klinge"?
    + 
 Does "Eric Manley" come before "Titus Klinge"?
    + 
 "Meredith Moore" and "Klinge, Titus"?
- 
 These decisions should be included in a **comparison function** and shouldn't affect the sorting algorithm

## Sorting in Python
- Python's built-in `sort` method and `sorted` function have two extra parameters:
    + 
 `key`: for specifying a comparison function
    + 
 `reverse`: for specifying whether you'd like the list sorted in ascending or descending order

```py
compare = lambda s1, s2: s1.lower() < s2.lower()
names.sort(key=compare, reverse=True)
```

## Sorting in Java
- Java's built-in `Arrays.sort` method supports using a `Comparator`

```java
Comparator<String> cmp = new Comparator<String>() {
    @Override
    public int compare(String s1, String s2) {
        s1 = s1.toLowerCase();
        s2 = s2.toLowerCase();
        return s1.compareTo(s2);
    }
}
Arrays.sort(names, cmp);
```

```java
Arrays.sort(names,
    (String s1, String s2) ->
        s1.toLowerCase().compareTo(s2.toLowerCase()));
```

## Selection Sort

- **Key idea**:
    + Repeatedly find smallest element
- 
 **Pseudocode**:
    + 
 For $i = 1$ to $n$ 
    + 
 Find smallest of elements $1\ldots i$
    + 
 Move that element to the $i$th position
- 
 What is the time-complexity?
    + 
 Depends!

</div>
<div>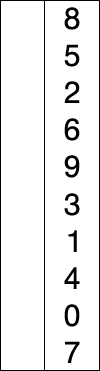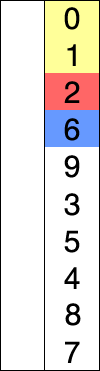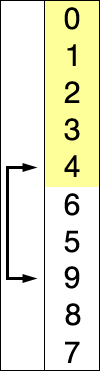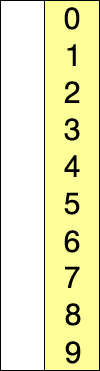

![selection sort animation](https://upload.wikimedia.org/wikipedia/commons/9/94/Selection-Sort-Animation.gif)

</div>
</div>

## Selection Sort
- **Given an array of $n$ elements**:
    + For $i = 1$ to $n$:
        * Find smallest of elements $1\ldots i$
        * Move that element to the $i$th position

---

- 
 Normally this algorithm would take $O(n^2)$ since finding the smallest element takes $O(n)$ time
- 
 Can we make this faster by using a data structure?

# Heapsort