reveal.js

# Heapsort

---

CS 137 // 2021-09-27

## Administrivia
- You should have turned in:
    + Your solution to daily exercise 6

# Questions
## ...about anything?

# Daily Exercise

# Sorting

## Why sorting?
1. Computers spend a lot of time sorting, historically 25% on mainframes
2. Sorting is an excellent problem to study in CS since there are many algorithms known
3. Many other algorithms depend on sorting or can be reduced to the sorting problem

## Selection Sort

- **Key idea**:
    + Repeatedly find smallest element
- 
 **Pseudocode**:
    + 
 For $i = 0$ to $n-1$ 
    + 
 Find smallest of elements $i\ldots n-1$
    + 
 Move that element to the $i$th position
- 
 What is the time-complexity?
    + 
 Depends!

</div>
<div>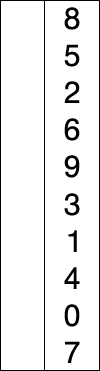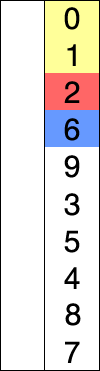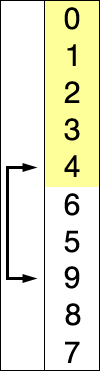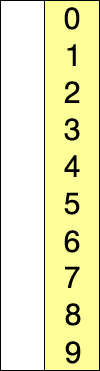

![selection sort animation](https://upload.wikimedia.org/wikipedia/commons/9/94/Selection-Sort-Animation.gif)

</div>
</div>

## Selection Sort
- **Given an array of $n$ elements**:
    + For $i = 0$ to $n-1$:
        * Find smallest of elements $i\ldots n-1$
        * Move that element to the $i$th position

---

- 
 Normally this algorithm would take $O(n^2)$ since finding the smallest element takes $O(n)$ time
- 
 But this can be sped up using a different data structure

# Heaps

## Heaps
- A **heap** is a data structure that efficiently supports the following operations:
    1. `extract_min`: removes the minimum element
    2. `insert`: adds a new element
- 
 In brief, a heap is a **binary tree** that satisfies the following property:
    + For every node `n`, the value of `n` is less than the value of all its descendants

## Heaps
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="290pt" height="188pt"
 viewBox="0.00 0.00 290.19 188.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 184)">
<title>dfa</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-184 286.19,-184 286.19,4 -4,4"/>

<g id="node1" class="node">
<title>100</title>
<ellipse fill="none" stroke="black" cx="140.6" cy="-162" rx="28.7" ry="18"/>
<text text-anchor="middle" x="140.6" y="-158.3" font-family="Times,serif" font-size="14.00">100</text>
</g>

<g id="node2" class="node">
<title>120</title>
<ellipse fill="none" stroke="black" cx="103.6" cy="-90" rx="28.7" ry="18"/>
<text text-anchor="middle" x="103.6" y="-86.3" font-family="Times,serif" font-size="14.00">120</text>
</g>

<g id="edge1" class="edge">
<title>100->120</title>
<path fill="none" stroke="black" d="M132.02,-144.76C127.6,-136.4 122.11,-126.02 117.13,-116.61"/>
<polygon fill="black" stroke="black" points="120.16,-114.84 112.39,-107.63 113.97,-118.11 120.16,-114.84"/>
</g>

<g id="node3" class="node">
<title>200</title>
<ellipse fill="none" stroke="black" cx="178.6" cy="-90" rx="28.7" ry="18"/>
<text text-anchor="middle" x="178.6" y="-86.3" font-family="Times,serif" font-size="14.00">200</text>
</g>

<g id="edge2" class="edge">
<title>100->200</title>
<path fill="none" stroke="black" d="M149.41,-144.76C154.02,-136.28 159.75,-125.71 164.92,-116.2"/>
<polygon fill="black" stroke="black" points="168.14,-117.61 169.83,-107.15 161.98,-114.27 168.14,-117.61"/>
</g>

<g id="node4" class="node">
<title>125</title>
<ellipse fill="none" stroke="black" cx="28.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="28.6" y="-14.3" font-family="Times,serif" font-size="14.00">125</text>
</g>

<g id="edge3" class="edge">
<title>120->125</title>
<path fill="none" stroke="black" d="M88.06,-74.5C77.43,-64.58 63.16,-51.26 51.27,-40.16"/>
<polygon fill="black" stroke="black" points="53.56,-37.51 43.86,-33.25 48.78,-42.63 53.56,-37.51"/>
</g>

<g id="node5" class="node">
<title>500</title>
<ellipse fill="none" stroke="black" cx="103.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="103.6" y="-14.3" font-family="Times,serif" font-size="14.00">500</text>
</g>

<g id="edge4" class="edge">
<title>120->500</title>
<path fill="none" stroke="black" d="M103.6,-71.7C103.6,-63.98 103.6,-54.71 103.6,-46.11"/>
<polygon fill="black" stroke="black" points="107.1,-46.1 103.6,-36.1 100.1,-46.1 107.1,-46.1"/>
</g>

<g id="node6" class="node">
<title>250</title>
<ellipse fill="none" stroke="black" cx="178.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="178.6" y="-14.3" font-family="Times,serif" font-size="14.00">250</text>
</g>

<g id="edge5" class="edge">
<title>200->250</title>
<path fill="none" stroke="black" d="M178.6,-71.7C178.6,-63.98 178.6,-54.71 178.6,-46.11"/>
<polygon fill="black" stroke="black" points="182.1,-46.1 178.6,-36.1 175.1,-46.1 182.1,-46.1"/>
</g>

<g id="node7" class="node">
<title>300</title>
<ellipse fill="none" stroke="black" cx="253.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="253.6" y="-14.3" font-family="Times,serif" font-size="14.00">300</text>
</g>

<g id="edge6" class="edge">
<title>200->300</title>
<path fill="none" stroke="black" d="M194.14,-74.5C204.77,-64.58 219.03,-51.26 230.92,-40.16"/>
<polygon fill="black" stroke="black" points="233.41,-42.63 238.33,-33.25 228.64,-37.51 233.41,-42.63"/>
</g>
</g>
</svg>

</div>

---

- 
 Notice that the minimum element is always the root
- 
 We will see that removing/inserting an element requires $O(\log n)$ time to repair it back into a heap

## Implementing a Heap
```java
class Node<E extends Comparable<E>> {
    E value;
    Node<E> left;
    Node<E> right;
}
```

- It is tempting to use a linked implementation similar to our binary search tree implementation
    + 
 This was nice before because self-balancing trees require moving entire subtrees around
- 
 We wont need to do this with heaps which enables us to use an even more efficient implementation

## Implementing a Heap
- Can we implement a heap with an **array**?
    + If so, how would we arrange the elements?

</div>

## Implementing a Heap
- For convenience, assume the start of the array has index 1
- Now, given the index of a node, how can we:
    + Find itsl eft subchild
    + 
 Find its right subchild
    + 
 Find its parent
    + 
 Determine if it is the root

## Implementing a Heap
- If array indices start at 1, then we can do:
    ```java
    int left_child(int k) {
        return 2 * k;
    }

int right_child(int k) {
        return 2 * k + 1;
    }

int parent(int k) {
        return k/2;     // integer division
    }

boolean is_root(int k) {
        return k == 1;
    }
    ```

## Implementing a Heap

```java
class Heap<E extends Comparable<E>> {
    E[] arr;
    int size;
}
```

## Implementing a Heap
- If we use this array-based implementation, how much space would the following heap consume?
    + 
 Assume that there are $n$ nodes in the heap
- 
 If we don't enforce that the tree is "complete," then lots of indices will be blank!
- 
 **Solution:** Make sure that every level is as full as possible at all times

## Exercises
- What is the time-complexity for:
    1. Checking if an arbitrary element is in a heap?
    2. 
 Finding the *largest* element?

## Inserting an Element
- Suppose I have a heap like the following and want to insert a new value 150 into it

</div>

## Inserting an Element
```java
void heap_insert(Heap<E> heap, E value) {
    if (is_full(heap)) {
        reallocate(heap);   // double its capacity
    }
        heap.size += 1;
    heap.arr[heap.size] = value;
    bubble_up(heap, heap.size);
}
```

## Inserting an Element
```java
void bubble_up(Heap<E> heap, int k) {
    if (is_root(k)) {
        return; // at root, nothing to do
    }

if (heap.arr[parent(k)] > heap.arr[k]) {
        swap(heap, k, parent(k));
        bubble_up(heap, parent(k));
    }
}
```

- 
 What is the time-complexity of `bubble_up`?

## Creating a Heap
- To create a heap from an array of elements, we just need to repeatedly insert them into a heap

```java
Heap<E> make_heap(E[] elements) {
    Heap<E> heap = new Heap<E>();
    for (int i = 0; i < elements.length; i++) {
        heap_insert(heap, elements[i]);
    }
    return heap;
}
```

- 
 What is the time-complexity of creating a heap?

## Extracting the Minimum
- Removing the root leaves a hole in the array
- 
 Instead of removing it directly, let's swap it with the right-most element and then "bubble down"

```java
E extract_min(Heap<E> heap) {
    if (heap.size == 0) {
        return null;    // heap is empty
    } else {
        E min = heap.arr[1];
        heap.arr[1] = heap.arr[heap.size];
        heap.size -= 1;
        bubble_down(heap, 1);
    }
}
```

## Extracting the Minimum

```java
void bubble_down(Heap<E> heap, int k) {
    int min = k;
    if (left_child(k) <= heap.size
            && heap.arr[left_child(k)] < heap.arr[min]) {
        min_index = left_child(k);
    }
    if (right_child(k) <= heap.size
            && heap.arr[right_child(k)] < heap.arr[min]) {
        min_index = right_child(k);
    }
    if (min != k) {
        swap(heap, k, min);
        bubble_down(heap, min);
    }
}
```

# Heapsort