reveal.js

# Merge Sort and Quick Sort

---

CS 137 // 2021-09-29

## Administrivia
- You should have turned in:
    + Your reflection for daily exercise 6

# Questions
## ...about anything?

# Heap Sort

## Heaps
- A **heap** is a data structure that efficiently supports the following operations:
    1. `extract_min`: removes the minimum element
    2. `insert`: adds a new element
- 
 A heap can be thought of as a **binary tree** that satisfies the following property:
    + For every node `n`, the value of `n` is less than the value of all its descendants

## Heaps
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="290pt" height="188pt"
 viewBox="0.00 0.00 290.19 188.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 184)">
<title>dfa</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-184 286.19,-184 286.19,4 -4,4"/>

<g id="node1" class="node">
<title>100</title>
<ellipse fill="none" stroke="black" cx="140.6" cy="-162" rx="28.7" ry="18"/>
<text text-anchor="middle" x="140.6" y="-158.3" font-family="Times,serif" font-size="14.00">100</text>
</g>

<g id="node2" class="node">
<title>120</title>
<ellipse fill="none" stroke="black" cx="103.6" cy="-90" rx="28.7" ry="18"/>
<text text-anchor="middle" x="103.6" y="-86.3" font-family="Times,serif" font-size="14.00">120</text>
</g>

<g id="edge1" class="edge">
<title>100->120</title>
<path fill="none" stroke="black" d="M132.02,-144.76C127.6,-136.4 122.11,-126.02 117.13,-116.61"/>
<polygon fill="black" stroke="black" points="120.16,-114.84 112.39,-107.63 113.97,-118.11 120.16,-114.84"/>
</g>

<g id="node3" class="node">
<title>200</title>
<ellipse fill="none" stroke="black" cx="178.6" cy="-90" rx="28.7" ry="18"/>
<text text-anchor="middle" x="178.6" y="-86.3" font-family="Times,serif" font-size="14.00">200</text>
</g>

<g id="edge2" class="edge">
<title>100->200</title>
<path fill="none" stroke="black" d="M149.41,-144.76C154.02,-136.28 159.75,-125.71 164.92,-116.2"/>
<polygon fill="black" stroke="black" points="168.14,-117.61 169.83,-107.15 161.98,-114.27 168.14,-117.61"/>
</g>

<g id="node4" class="node">
<title>125</title>
<ellipse fill="none" stroke="black" cx="28.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="28.6" y="-14.3" font-family="Times,serif" font-size="14.00">125</text>
</g>

<g id="edge3" class="edge">
<title>120->125</title>
<path fill="none" stroke="black" d="M88.06,-74.5C77.43,-64.58 63.16,-51.26 51.27,-40.16"/>
<polygon fill="black" stroke="black" points="53.56,-37.51 43.86,-33.25 48.78,-42.63 53.56,-37.51"/>
</g>

<g id="node5" class="node">
<title>500</title>
<ellipse fill="none" stroke="black" cx="103.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="103.6" y="-14.3" font-family="Times,serif" font-size="14.00">500</text>
</g>

<g id="edge4" class="edge">
<title>120->500</title>
<path fill="none" stroke="black" d="M103.6,-71.7C103.6,-63.98 103.6,-54.71 103.6,-46.11"/>
<polygon fill="black" stroke="black" points="107.1,-46.1 103.6,-36.1 100.1,-46.1 107.1,-46.1"/>
</g>

<g id="node6" class="node">
<title>250</title>
<ellipse fill="none" stroke="black" cx="178.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="178.6" y="-14.3" font-family="Times,serif" font-size="14.00">250</text>
</g>

<g id="edge5" class="edge">
<title>200->250</title>
<path fill="none" stroke="black" d="M178.6,-71.7C178.6,-63.98 178.6,-54.71 178.6,-46.11"/>
<polygon fill="black" stroke="black" points="182.1,-46.1 178.6,-36.1 175.1,-46.1 182.1,-46.1"/>
</g>

<g id="node7" class="node">
<title>300</title>
<ellipse fill="none" stroke="black" cx="253.6" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="253.6" y="-14.3" font-family="Times,serif" font-size="14.00">300</text>
</g>

<g id="edge6" class="edge">
<title>200->300</title>
<path fill="none" stroke="black" d="M194.14,-74.5C204.77,-64.58 219.03,-51.26 230.92,-40.16"/>
<polygon fill="black" stroke="black" points="233.41,-42.63 238.33,-33.25 228.64,-37.51 233.41,-42.63"/>
</g>
</g>
</svg>

</div>

---

- The minimum element is always the root

## Heaps
- We can implement heaps using an **array**
- 
 Inserting an element is $O(\log n)$
    + Add at the bottom and "bubble it up"
- 
 Removing the min is $O(\log n)$
    + Move last item to the root and "bubble it down"

## Heap Sort

```java
void heap_sort(E[] elements) {
    Heap<E> heap = make_heap(elements);
    for (int i = 0; i < elements.length; i++) {
        elements[i] = extract_min(heap);
    }
}
```

- 
 What's the runtime complexity?
    + 
 $O(n \log n)$

## Heap Sort: Debrief
- Heap sort is literally the same algorithm as selection sort with a clever use of a data structure
- **Takeaway**: Using the right data structure in the right place can yield **huge** runtime improvements!
- 
 Knowing about common data structures and how to employ them is a big component of this course

# Merge Sort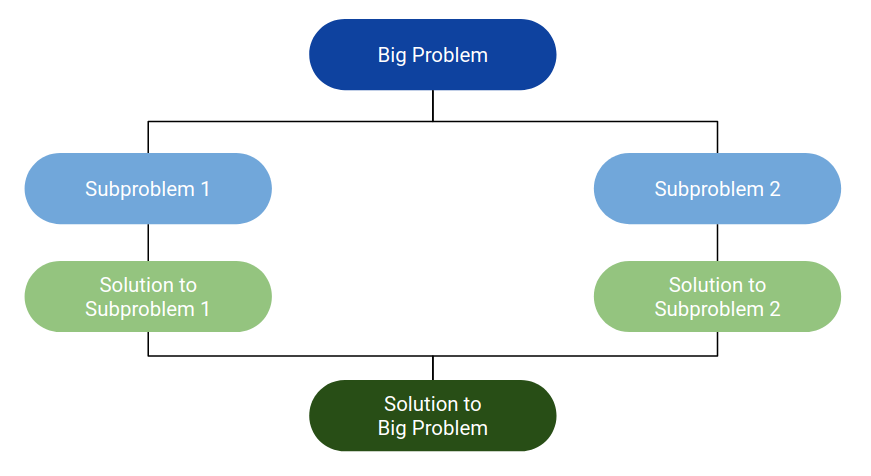

## Divide and Conquer

![split big problem into subproblems](/teaching/2021f/cs137/assets/images/divide-and-conquer.png)

## Merge Sort

- **Key idea:**
    + Divide the list into two halves
    + Recursively sort each independently
    + Merge the two sorted lists together

![merge sort animation](https://upload.wikimedia.org/wikipedia/commons/c/cc/Merge-sort-example-300px.gif)

## Implementation

```py
def merge_sort(elements):
    if len(elements) > 1:
        mid = len(elements) // 2
        left_half = elements[:mid]
        right_half = elements[mid:]

merge_sort(left_half)
        merge_sort(right_half)
        merge(left_half, right_half, elements)
```

## Merging

```py
def merge(src1, src2, dst):
    i1, i2, i3 = 0, 0, 0
    
    # while both lists at least have one element
    while i1 < len(src1) and i2 < len(src2):
        if src1[i1] < src2[i2]:
            dst[i3] = src1[i1]
            i1 = i1 + 1
            i3 = i3 + 1
        else:
            dst[i3] = src2[i2]
            i2 = i2 + 1
            i3 = i3 + 1
    
    # Copy the remaining elements into the destination
    dst[i3:] = src1[i1:] + src2[i2:]

```

## Visualization of Merge Sort

# Quick Sort

## Quick Sort
- **Key idea**:
    + Select a *pivot* element
    + Partition the array so that elements $\le$ the pivot are on the left and elements $>$ are on the right
    + Recursively sort each part

![quick sort animation](https://upload.wikimedia.org/wikipedia/commons/9/9c/Quicksort-example.gif)

## Implementation
```py
def quick_sort(arr, left, right):
    if left < right:
        mid = partition(arr, left, right)
        quick_sort(arr, left, mid-1)
        quick_sort(arr, mid+1, right)

def partition(arr, left, right):
    pivot = arr[right]
    i = left-1
    for j in range(left, right+1):
        if arr[j] <= pivot:
            i = i+1
            arr[i], arr[j] = arr[j], arr[i]
    return i
```

## Visualization of Quick Sort

## Quick Sort Analysis
- What is the worst-case running time of quick sort?
    + 
 $O(n^2)$
- 
 If we **randomly** select a pivot, with high probability it will be "near" the center
    + 
 Expected runtime becomes $O(n\log n)$
- 
 **Takeaway:** Randomness is another tool that can speed up algorithms significantly

## Comparison of Sorts
- Merge sort is a great **distributed** sorting algorithm
    + 
 Can be parallelized
    + 
 Works well even on massive datasets distributed across many servers
- 
 Quick sort performs amazingly well on datasets that can fit into RAM in one giant array
    + 
 Makes great use of the cache
    + 
 Does not use much extra memory
    + 
 Usually 2-3 times faster in these situations