reveal.js

# Divide and Conquer

---

CS 137 // 2021-10-04

## Administrivia
- You should have turned in:
    + Your solution for daily exercise 7

# Questions
## ...about anything?

# Daily Exercise 7

# Complexity of Sorting

## Complexity of Sorting
- The best sorting algorithms we've seen so far are $O(n \log n)$
- 
 Is it possible to do *better*?

## Comparison Sorts
- A *comparison* sort is a sorting algorithm that repeatedly compares two elements using some form of `<` operation
- 
 **Claim:** Any comparison sort requires $\Omega(n \log n)$ comparisons

## Comparison Sort Complexity
- Note that we can represent a comparison sort algorithm as a **tree**
    + Leaves represent final, sorted, array
- 
 How many leaves are there?
    + 
 At least $n!$ (otherwise two input permutations would terminate with the same leaf)
- 
 **Lemma:** $n! \ge \left(\frac{n}{2}\right)^{\frac{n}{2}}$

## Proof of Claim
- Comparison sorting tree has $n!$ leaves
- 
 Assume that tree has height $k$
- 
 The shortest possible tree has $2^{k-1}$ leaves
- 
 $2^{k-1} \ge n! \ge \left(\frac{n}{2}\right)^{\frac{n}{2}}$
- 
 $\log_2(2^{k-1}) \ge log_2 \left(\frac{n}{2}\right)^{\frac{n}{2}}$
- 
 $k-1 \ge \frac{n}{2} \log_2(\frac{n}{2})$
- 
 $k = \Omega(n\log n)$

## Non-Comparison Sorts
- Only way to do better than $\Theta(n\log n)$ is to avoid comparing elements
- 
 How is this possible?
- 
 Suppose that I am sorting an array of 0s and 1s
    + Can we sort this faster than $O(n \log n)$?

## Radix Sort
- **Key idea:** Sort elements by digits
    + Group them all by their most significant digit
    + 
 Then by their next significant digit
    + 
 Until they are sorted
- 
 Works on strings, too
- 
 Runtime is $O(nw)$ where $w$ is the "length" of the elements
    + 
 Numerical data bounded by 64 bits makes the algorithm $O(n)$ time

# Divide and Conquer

## Divide and Conquer

![split big problem into subproblems](/teaching/2021f/cs137/assets/images/divide-and-conquer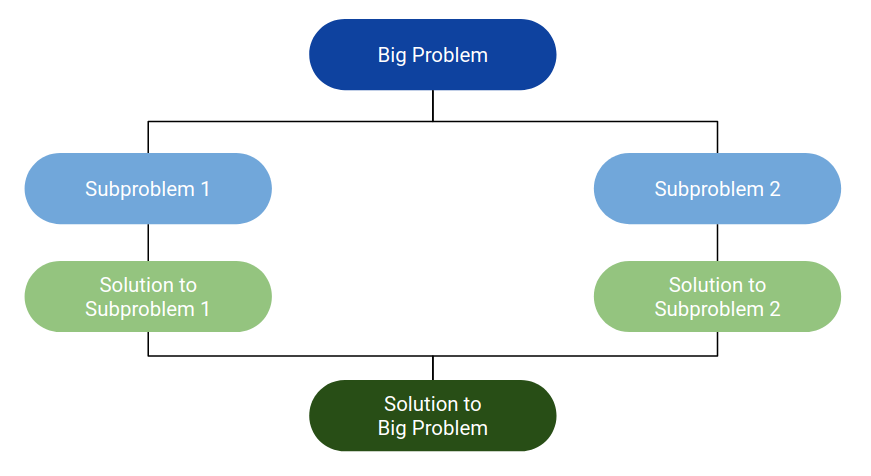.png)

## Fast Heap Construction
- Recall that we wrote an algorithm to construct a heap in $O(n\log n)$ time
    ```java
    Heap<E> make_heap(E[] elements) {
        Heap<E> heap = new Heap<E>();
        for (int i = 0; i < elements.length; i++) {
            heap_insert(heap, elements[i]);
        }
        return heap;
    }
    ```
- 
 Can we do better?

## Fast Heap Construction
- **Key idea:** Divide the elements in half and create two heaps of size $\frac{n}{2}$ and combine them
- 
 If we make both heaps children of a root node, it takes $O(\log n)$ time to bubble down the root
- 
 Runtime can be expressed as a **recurrence relation**
    + $T(n) = 2T(\frac{n}{2}) + O(\log n)$

# Recurrence Relations

## Recurrence Relations
- All divide and conquer algorithms have runtimes that are easiest to express with a recurrence relation
    + $T(n) = a\cdot T(\frac{n}{b}) + f(n)$
- 
 **Binary Search:**
    + 
 $T(n) = T(\frac{n}{2}) + O(1)$
- 
 **Merge Sort:**
    + 
 $T(n) = 2T(\frac{n}{2}) + O(n)$

## Exercise 1
- Given two sorted arrays $A$ and $B$ of size $n$ and $m$ respectively, find the median of the elements.
- 
 *Hint:* You can do better than $O(n)$-time!

## Exercise 2
- Given an unsorted array $A$ of $n$ elements, find the $k$th smallest element of $A$
- 
 *Hint:* You can do better than $O(n\log n)$-time!