reveal.js

# Master Theorem

---

CS 137 // 2021-10-06

## Administrivia
- You should have turned in:
    + You reflection for daily exercise 7
    + Your solution for daily exercise 8

# Exam 1
- Monday, October 11th

## Exam 1
- **Format of the exam**:
    + Written, in-class, 75-minute exam
    + Closed textbook/notes/internet
- 
 **Topics**: (Skiena Chapters 1-5)
    + Asymptotic notation, data structures, trees, hashtables, sorting, and divide and conquer
- 
 Problems on exam will be directly taken or directly inspired from exercises at the end of each chapter

# Questions
## ...about anything?

# Daily Exercise 8

# Divide and Conquer

## Divide and Conquer

![split big problem into subproblems](/teaching/2021f/cs137/assets/images/divide-and-conquer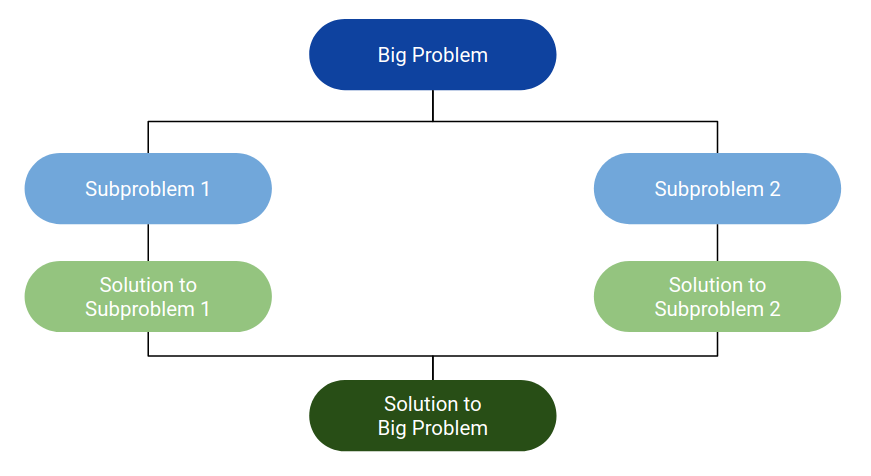.png)

## Recurrence Relations
- All divide and conquer algorithms have runtimes that are easiest to express with a recurrence relation
    + $T(n) = a\cdot T(\frac{n}{b}) + f(n)$
- 
 **Binary Search:**
    + $T(n) = T(\frac{n}{2}) + O(1)$
- 
 **Merge Sort:**
    + $T(n) = 2T(\frac{n}{2}) + O(n)$
- 
 **Make Heap:**
    + $T(n) = 2T(\frac{n}{2}) + O(\log n)$

# Master Theorem

## Master Theorem
- If a divide and conquer algorithm's runtime is:
    + $T(n) = a\cdot T(\frac{n}{b}) + f(n)$
- Then we have three cases:
    1. 
 If $f(n) = O(n^{\log_b(a-\epsilon)})$ for some $\epsilon > 0$
        + Then $T(n) = \Theta(n^{\log_b a})$
    2. 
 If $f(n) = \Theta(n^{\log_b a})$
        + Then $T(n) = \Theta(n^{\log_b a} \log n)$
    3. 
 If $f(n) = \Omega(n^{\log_b(a + \epsilon)})$ for some $\epsilon > 0$
        + Then $T(n) = \Theta(f(n))$

## Case 1: Leaves Dominate

- Suppose we have an algorithm that runs in:
    + $T(n) = 3\cdot T(\frac{n}{2}) + n$

---

- 
 Since $\log_2 3 = 1.585$, we have $f(n) = O(n^{\log_2 3})$
- 
 Thus, case 1 of the MT says that $T(n) = \Theta(n^{\log_2 3})$

## Case 1: Leaves Dominate
$$T(n) = a\cdot T(\frac{n}{b}) + f(n)$$

---

- If we have:
    + $f(n) = O(n^{\log_b(a-\epsilon)})$ for some $\epsilon > 0$
- Then it means that $f(n)$ is small enough that the runtime is bounded by the number of leaves of the recursion tree

## Case 2: Balanced
- Suppose we have an algorithm that runs in:
    + $T(n) = 2\cdot T(\frac{n}{2}) + 2n$

---

- 
 Since $\log_2 2 = 1$, we have $f(n) = \Theta(n)$
- 
 Case 2 of the MT says that $T(n) = \Theta(n\log n)$

## Case 3: Root Dominates
- Suppose we have an algorithm that runs in:
    + $T(n) = 2\cdot T(\frac{n}{2}) + n^2$

---

- 
 Since we have $f(n) = \Omega(n^{1+\epsilon})$
- 
 Case 3 of the MT says that $T(n) = \Theta(n^2)$

## Exercise 1
- Apply the master theorem to each of the following recurrences:
    - 
 $T(n) = 4T(\frac{n}{2}) + n^2$
    - 
 $T(n) = 4T(\frac{n}{2}) + n$
    - 
 $T(n) = 4T(\frac{n}{2}) + n^3$
    - 
 $T(n) = T(n-1) + T(n-2) + 1$

## Exercise 2
- What of the master theorem do each of the following fall into?
- 
 **Binary Search:**
    + $T(n) = T(\frac{n}{2}) + O(1)$
- 
 **Merge Sort:**
    + $T(n) = 2T(\frac{n}{2}) + O(n)$
- 
 **Make Heap:**
    + $T(n) = 2T(\frac{n}{2}) + O(\log n)$

# Exam Practice