reveal.js

## Introduction to
# Graphs

---

CS 137 // 2021-10-13

## Administrivia
- Exam 1 debrief

# Questions
## ...about anything?

# Graphs

## Graph Definition
- A **graph** is a linked data structure consisting of:
    1. 
 A set $V$ of nodes referred to as **vertices**
    2. 
 A set $E$ of **edges** linking vertices together
- 
 Sometimes we write $G = (V,E)$

## Graph Definition

</div>

---

- 
 $V = \\{a, b, c, d, e\\}$
- 
 $E = \\{(a,b),(b,c),(a,c),(d,c),(c,e),(e,a)\\}$

# Examples

## Dependency Graphs

<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="486pt" height="342pt"
 viewBox="0.00 0.00 486.00 342.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 338)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-338 482,-338 482,4 -4,4"/>

<g id="node1" class="node">
<title>cs147</title>
<polygon fill="none" stroke="black" points="166,-186 86,-186 86,-148 166,-148 166,-186"/>
<text text-anchor="middle" x="126" y="-170.8" font-family="Times,serif" font-size="14.00">CS 147</text>
<text text-anchor="middle" x="126" y="-155.8" font-family="Times,serif" font-size="14.00">Graphics</text>
</g>

<g id="node2" class="node">
<title>cs167</title>
<polygon fill="none" stroke="black" points="286,-260 176,-260 176,-222 286,-222 286,-260"/>
<text text-anchor="middle" x="231" y="-244.8" font-family="Times,serif" font-size="14.00">CS 167</text>
<text text-anchor="middle" x="231" y="-229.8" font-family="Times,serif" font-size="14.00">Mach. Learn.</text>
</g>

<g id="node3" class="node">
<title>cs178</title>
<polygon fill="none" stroke="black" points="252,-186 184,-186 184,-148 252,-148 252,-186"/>
<text text-anchor="middle" x="218" y="-170.8" font-family="Times,serif" font-size="14.00">CS 178</text>
<text text-anchor="middle" x="218" y="-155.8" font-family="Times,serif" font-size="14.00">Cloud</text>
</g>

<g id="node4" class="node">
<title>cs65</title>
<polygon fill="lightblue" stroke="lightblue" points="260.5,-334 201.5,-334 201.5,-296 260.5,-296 260.5,-334"/>
<text text-anchor="middle" x="231" y="-318.8" font-family="Times,serif" font-size="14.00">CS 65</text>
<text text-anchor="middle" x="231" y="-303.8" font-family="Times,serif" font-size="14.00">CS I</text>
</g>

<g id="edge1" class="edge">
<title>cs65->cs167</title>
<path fill="none" stroke="black" d="M231,-295.83C231,-288.13 231,-278.97 231,-270.42"/>
<polygon fill="black" stroke="black" points="234.5,-270.41 231,-260.41 227.5,-270.41 234.5,-270.41"/>
</g>

<g id="node5" class="node">
<title>cs66</title>
<polygon fill="lightblue" stroke="lightblue" points="157.5,-260 98.5,-260 98.5,-222 157.5,-222 157.5,-260"/>
<text text-anchor="middle" x="128" y="-244.8" font-family="Times,serif" font-size="14.00">CS 66</text>
<text text-anchor="middle" x="128" y="-229.8" font-family="Times,serif" font-size="14.00">CS II</text>
</g>

<g id="edge2" class="edge">
<title>cs65->cs66</title>
<path fill="none" stroke="black" d="M205.01,-295.83C192.08,-286.79 176.28,-275.75 162.36,-266.02"/>
<polygon fill="black" stroke="black" points="164.18,-263.02 153.98,-260.16 160.17,-268.76 164.18,-263.02"/>
</g>

<g id="node14" class="node">
<title>cs139</title>
<polygon fill="lightseagreen" stroke="lightseagreen" points="372,-260 304,-260 304,-222 372,-222 372,-260"/>
<text text-anchor="middle" x="338" y="-244.8" font-family="Times,serif" font-size="14.00">CS 139</text>
<text text-anchor="middle" x="338" y="-229.8" font-family="Times,serif" font-size="14.00">Theory</text>
</g>

<g id="edge3" class="edge">
<title>cs65->cs139</title>
<path fill="none" stroke="black" d="M258,-295.83C271.43,-286.79 287.85,-275.75 302.3,-266.02"/>
<polygon fill="black" stroke="black" points="304.67,-268.65 311.01,-260.16 300.76,-262.84 304.67,-268.65"/>
</g>

<g id="edge4" class="edge">
<title>cs66->cs147</title>
<path fill="none" stroke="black" d="M127.5,-221.83C127.28,-214.13 127.03,-204.97 126.79,-196.42"/>
<polygon fill="black" stroke="black" points="130.29,-196.31 126.51,-186.41 123.29,-196.51 130.29,-196.31"/>
</g>

<g id="edge5" class="edge">
<title>cs66->cs178</title>
<path fill="none" stroke="black" d="M150.71,-221.83C161.8,-212.96 175.3,-202.16 187.29,-192.57"/>
<polygon fill="black" stroke="black" points="189.67,-195.14 195.3,-186.16 185.3,-189.68 189.67,-195.14"/>
</g>

<g id="node6" class="node">
<title>cs146</title>
<polygon fill="lightblue" stroke="lightblue" points="329.5,-186 270.5,-186 270.5,-148 329.5,-148 329.5,-186"/>
<text text-anchor="middle" x="300" y="-170.8" font-family="Times,serif" font-size="14.00">CS 67</text>
<text text-anchor="middle" x="300" y="-155.8" font-family="Times,serif" font-size="14.00">CS III</text>
</g>

<g id="edge6" class="edge">
<title>cs66->cs146</title>
<path fill="none" stroke="black" d="M157.72,-226.04C160.84,-224.64 163.98,-223.27 167,-222 208.22,-204.62 219.78,-203.38 261,-186 261.09,-185.96 261.19,-185.92 261.28,-185.88"/>
<polygon fill="black" stroke="black" points="262.51,-189.16 270.28,-181.96 259.71,-182.75 262.51,-189.16"/>
</g>

<g id="node7" class="node">
<title>cs130</title>
<polygon fill="lightblue" stroke="lightblue" points="68,-186 0,-186 0,-148 68,-148 68,-186"/>
<text text-anchor="middle" x="34" y="-170.8" font-family="Times,serif" font-size="14.00">CS 130</text>
<text text-anchor="middle" x="34" y="-155.8" font-family="Times,serif" font-size="14.00">Org I</text>
</g>

<g id="edge7" class="edge">
<title>cs66->cs130</title>
<path fill="none" stroke="black" d="M104.28,-221.83C92.59,-212.88 78.33,-201.96 65.72,-192.3"/>
<polygon fill="black" stroke="black" points="67.78,-189.47 57.71,-186.16 63.52,-195.02 67.78,-189.47"/>
</g>

<g id="node8" class="node">
<title>cs135</title>
<polygon fill="lightblue" stroke="lightblue" points="334,-112 266,-112 266,-74 334,-74 334,-112"/>
<text text-anchor="middle" x="300" y="-96.8" font-family="Times,serif" font-size="14.00">CS 135</text>
<text text-anchor="middle" x="300" y="-81.8" font-family="Times,serif" font-size="14.00">PL</text>
</g>

<g id="edge8" class="edge">
<title>cs146->cs135</title>
<path fill="none" stroke="black" d="M300,-147.83C300,-140.13 300,-130.97 300,-122.42"/>
<polygon fill="black" stroke="black" points="303.5,-122.41 300,-112.41 296.5,-122.41 303.5,-122.41"/>
</g>

<g id="node9" class="node">
<title>cs137</title>
<polygon fill="lightblue" stroke="lightblue" points="447.5,-112 352.5,-112 352.5,-74 447.5,-74 447.5,-112"/>
<text text-anchor="middle" x="400" y="-96.8" font-family="Times,serif" font-size="14.00">CS 137</text>
<text text-anchor="middle" x="400" y="-81.8" font-family="Times,serif" font-size="14.00">Algorithms</text>
</g>

<g id="edge9" class="edge">
<title>cs146->cs137</title>
<path fill="none" stroke="black" d="M325.23,-147.83C337.79,-138.79 353.13,-127.75 366.64,-118.02"/>
<polygon fill="black" stroke="black" points="368.7,-120.85 374.77,-112.16 364.61,-115.17 368.7,-120.85"/>
</g>

<g id="node13" class="node">
<title>cs188</title>
<polygon fill="lightblue" stroke="lightblue" points="248,-112 180,-112 180,-74 248,-74 248,-112"/>
<text text-anchor="middle" x="214" y="-96.8" font-family="Times,serif" font-size="14.00">CS 188</text>
<text text-anchor="middle" x="214" y="-81.8" font-family="Times,serif" font-size="14.00">SE</text>
</g>

<g id="edge10" class="edge">
<title>cs146->cs188</title>
<path fill="none" stroke="black" d="M278.3,-147.83C267.81,-139.05 255.05,-128.37 243.68,-118.85"/>
<polygon fill="black" stroke="black" points="245.61,-115.9 235.69,-112.16 241.12,-121.27 245.61,-115.9"/>
</g>

<g id="node10" class="node">
<title>cs191</title>
<polygon fill="lightblue" stroke="lightblue" points="255.5,-38 172.5,-38 172.5,0 255.5,0 255.5,-38"/>
<text text-anchor="middle" x="214" y="-22.8" font-family="Times,serif" font-size="14.00">CS 191</text>
<text text-anchor="middle" x="214" y="-7.8" font-family="Times,serif" font-size="14.00">Capstone</text>
</g>

<g id="node11" class="node">
<title>math54</title>
<polygon fill="lightblue" stroke="lightblue" points="397.5,-334 278.5,-334 278.5,-296 397.5,-296 397.5,-334"/>
<text text-anchor="middle" x="338" y="-318.8" font-family="Times,serif" font-size="14.00">MATH 54</text>
<text text-anchor="middle" x="338" y="-303.8" font-family="Times,serif" font-size="14.00">Discrete Math</text>
</g>

<g id="edge11" class="edge">
<title>math54->cs167</title>
<path fill="none" stroke="black" d="M311,-295.83C297.57,-286.79 281.15,-275.75 266.7,-266.02"/>
<polygon fill="black" stroke="black" points="268.24,-262.84 257.99,-260.16 264.33,-268.65 268.24,-262.84"/>
</g>

<g id="edge12" class="edge">
<title>math54->cs137</title>
<path fill="none" stroke="black" d="M356.85,-295.72C365.7,-285.98 375.49,-273.28 381,-260 399.86,-214.55 402.06,-156.44 401.41,-122.41"/>
<polygon fill="black" stroke="black" points="404.9,-122.15 401.11,-112.25 397.91,-122.35 404.9,-122.15"/>
</g>

<g id="edge13" class="edge">
<title>math54->cs139</title>
<path fill="none" stroke="black" d="M338,-295.83C338,-288.13 338,-278.97 338,-270.42"/>
<polygon fill="black" stroke="black" points="341.5,-270.41 338,-260.41 334.5,-270.41 341.5,-270.41"/>
</g>

<g id="node12" class="node">
<title>cs83</title>
<polygon fill="lightblue" stroke="lightblue" points="478,-334 416,-334 416,-296 478,-296 478,-334"/>
<text text-anchor="middle" x="447" y="-318.8" font-family="Times,serif" font-size="14.00">CS 83</text>
<text text-anchor="middle" x="447" y="-303.8" font-family="Times,serif" font-size="14.00">Ethics</text>
</g>

<g id="edge14" class="edge">
<title>cs188->cs191</title>
<path fill="none" stroke="black" d="M214,-73.83C214,-66.13 214,-56.97 214,-48.42"/>
<polygon fill="black" stroke="black" points="217.5,-48.41 214,-38.41 210.5,-48.41 217.5,-48.41"/>
</g>
</g>
</svg>

</div>

## Social Networks

<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="309pt" height="332pt"
 viewBox="0.00 0.00 309.09 332.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 328)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-328 305.09,-328 305.09,4 -4,4"/>

<g id="node1" class="node">
<title>Titus</title>
<ellipse fill="none" stroke="black" cx="181.95" cy="-234" rx="34.39" ry="18"/>
<text text-anchor="middle" x="181.95" y="-230.3" font-family="Times,serif" font-size="14.00">Titus</text>
</g>

<g id="node2" class="node">
<title>Tim</title>
<ellipse fill="none" stroke="black" cx="126.95" cy="-18" rx="28.7" ry="18"/>
<text text-anchor="middle" x="126.95" y="-14.3" font-family="Times,serif" font-size="14.00">Tim</text>
</g>

<g id="edge1" class="edge">
<title>Titus--Tim</title>
<path fill="none" stroke="black" d="M177.54,-215.85C167.21,-175.68 141.57,-75.89 131.3,-35.94"/>
</g>

<g id="node4" class="node">
<title>Adam</title>
<ellipse fill="none" stroke="black" cx="87.95" cy="-162" rx="37.09" ry="18"/>
<text text-anchor="middle" x="87.95" y="-158.3" font-family="Times,serif" font-size="14.00">Adam</text>
</g>

<g id="edge14" class="edge">
<title>Titus--Adam</title>
<path fill="none" stroke="black" d="M162.92,-218.83C146.72,-206.77 123.55,-189.51 107.26,-177.38"/>
</g>

<g id="node3" class="node">
<title>Meredith</title>
<ellipse fill="none" stroke="black" cx="53.95" cy="-306" rx="53.89" ry="18"/>
<text text-anchor="middle" x="53.95" y="-302.3" font-family="Times,serif" font-size="14.00">Meredith</text>
</g>

<g id="edge3" class="edge">
<title>Meredith--Titus</title>
<path fill="none" stroke="black" d="M80.78,-290.33C103.94,-277.66 137.05,-259.55 159,-247.55"/>
</g>

<g id="edge5" class="edge">
<title>Meredith--Tim</title>
<path fill="none" stroke="black" d="M44.4,-287.93C39.31,-277.82 33.56,-264.57 30.95,-252 14.6,-173.28 2.92,-137.92 48.95,-72 62.72,-52.27 86.4,-37.72 104.06,-28.91"/>
</g>

<g id="edge2" class="edge">
<title>Meredith--Adam</title>
<path fill="none" stroke="black" d="M50.41,-287.83C47.38,-269.58 44.54,-240.08 51.95,-216 56.2,-202.18 65.41,-188.73 73.46,-178.83"/>
</g>

<g id="node5" class="node">
<title>Eric</title>
<ellipse fill="none" stroke="black" cx="87.95" cy="-90" rx="29.8" ry="18"/>
<text text-anchor="middle" x="87.95" y="-86.3" font-family="Times,serif" font-size="14.00">Eric</text>
</g>

<g id="edge4" class="edge">
<title>Meredith--Eric</title>
<path fill="none" stroke="black" d="M48.1,-287.89C38.79,-257.73 23.41,-193.63 41.95,-144 47.66,-128.71 59.99,-114.9 70.45,-105.22"/>
</g>

<g id="node6" class="node">
<title>Reza</title>
<ellipse fill="none" stroke="black" cx="267.95" cy="-234" rx="33.29" ry="18"/>
<text text-anchor="middle" x="267.95" y="-230.3" font-family="Times,serif" font-size="14.00">Reza</text>
</g>

<g id="edge6" class="edge">
<title>Meredith--Reza</title>
<path fill="none" stroke="black" d="M93.62,-293.63C128.45,-283.43 180.38,-267.69 224.95,-252 230.55,-250.03 236.51,-247.77 242.14,-245.57"/>
</g>

<g id="node7" class="node">
<title>Rajin</title>
<ellipse fill="none" stroke="black" cx="94.95" cy="-234" rx="34.39" ry="18"/>
<text text-anchor="middle" x="94.95" y="-230.3" font-family="Times,serif" font-size="14.00">Rajin</text>
</g>

<g id="edge7" class="edge">
<title>Meredith--Rajin</title>
<path fill="none" stroke="black" d="M63.87,-288.05C70.41,-276.89 78.93,-262.34 85.39,-251.31"/>
</g>

<g id="edge8" class="edge">
<title>Adam--Eric</title>
<path fill="none" stroke="black" d="M87.95,-143.7C87.95,-132.85 87.95,-118.92 87.95,-108.1"/>
</g>

<g id="edge9" class="edge">
<title>Eric--Tim</title>
<path fill="none" stroke="black" d="M96.99,-72.76C103.29,-61.46 111.66,-46.44 117.95,-35.15"/>
</g>

<g id="edge13" class="edge">
<title>Reza--Tim</title>
<path fill="none" stroke="black" d="M257.35,-216.92C231.15,-177.16 163.6,-74.62 137.47,-34.98"/>
</g>

<g id="node8" class="node">
<title>Chris</title>
<ellipse fill="none" stroke="black" cx="181.95" cy="-306" rx="36" ry="18"/>
<text text-anchor="middle" x="181.95" y="-302.3" font-family="Times,serif" font-size="14.00">Chris</text>
</g>

<g id="edge10" class="edge">
<title>Chris--Titus</title>
<path fill="none" stroke="black" d="M181.95,-287.7C181.95,-276.85 181.95,-262.92 181.95,-252.1"/>
</g>

<g id="edge11" class="edge">
<title>Chris--Reza</title>
<path fill="none" stroke="black" d="M200.18,-290.15C214.98,-278.12 235.7,-261.25 250.32,-249.35"/>
</g>

<g id="edge12" class="edge">
<title>Chris--Rajin</title>
<path fill="none" stroke="black" d="M163.49,-290.15C148.63,-278.2 127.85,-261.47 113.07,-249.58"/>
</g>
</g>
</svg>

</div>

## City Maps

[Des Moines Maps](https://www.catchdesmoines.com/visitor-info/transportation/maps/)

# Other Examples?

# Flavors of Graphs

## Directed / Undirected
- A graph $G = (V,E)$ is an **undirected** graph if the edges are bidirectional
    + If $(a,b)\in E$, then $(b,a)\in E$
- Otherwise a graph is called **directed**

---

**Directed**
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="332pt" height="97pt"
 viewBox="0.00 0.00 332.00 96.53" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 92.53)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-92.53 328,-92.53 328,4 -4,4"/>

<g id="node1" class="node">
<title>a</title>
<ellipse fill="none" stroke="black" cx="27" cy="-24.53" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-20.83" font-family="Times,serif" font-size="14.00">a</text>
</g>

<g id="node2" class="node">
<title>b</title>
<ellipse fill="none" stroke="black" cx="117" cy="-70.53" rx="27" ry="18"/>
<text text-anchor="middle" x="117" y="-66.83" font-family="Times,serif" font-size="14.00">b</text>
</g>

<g id="edge1" class="edge">
<title>a->b</title>
<path fill="none" stroke="black" d="M48.85,-35.43C60.03,-41.27 74,-48.57 86.29,-55"/>
<polygon fill="black" stroke="black" points="84.81,-58.17 95.29,-59.7 88.05,-51.97 84.81,-58.17"/>
</g>

<g id="node3" class="node">
<title>c</title>
<ellipse fill="none" stroke="black" cx="207" cy="-32.53" rx="27" ry="18"/>
<text text-anchor="middle" x="207" y="-28.83" font-family="Times,serif" font-size="14.00">c</text>
</g>

<g id="edge3" class="edge">
<title>a->c</title>
<path fill="none" stroke="black" d="M54.26,-25.71C84.85,-27.08 135.55,-29.36 169.84,-30.9"/>
<polygon fill="black" stroke="black" points="169.77,-34.4 179.92,-31.35 170.08,-27.41 169.77,-34.4"/>
</g>

<g id="edge2" class="edge">
<title>b->c</title>
<path fill="none" stroke="black" d="M140.21,-60.94C150.63,-56.44 163.23,-50.99 174.61,-46.08"/>
<polygon fill="black" stroke="black" points="176.01,-49.29 183.8,-42.11 173.23,-42.86 176.01,-49.29"/>
</g>

<g id="node4" class="node">
<title>d</title>
<ellipse fill="none" stroke="black" cx="297" cy="-32.53" rx="27" ry="18"/>
<text text-anchor="middle" x="297" y="-28.83" font-family="Times,serif" font-size="14.00">d</text>
</g>

<g id="edge5" class="edge">
<title>c->d</title>
<path fill="none" stroke="black" d="M232.51,-26.4C241.4,-25.79 251.62,-25.63 261.22,-25.91"/>
<polygon fill="black" stroke="black" points="261.16,-29.41 271.31,-26.39 261.49,-22.42 261.16,-29.41"/>
</g>

<g id="edge6" class="edge">
<title>d->a</title>
<path fill="none" stroke="black" d="M275.76,-21.18C263.97,-15.24 248.6,-8.57 234,-5.53 174.2,6.93 102.93,-5.55 61.82,-15.33"/>
<polygon fill="black" stroke="black" points="60.92,-11.95 52.05,-17.75 62.6,-18.75 60.92,-11.95"/>
</g>

<g id="edge4" class="edge">
<title>d->c</title>
<path fill="none" stroke="black" d="M271.31,-38.66C262.41,-39.27 252.18,-39.43 242.59,-39.14"/>
<polygon fill="black" stroke="black" points="242.67,-35.64 232.51,-38.65 242.33,-42.63 242.67,-35.64"/>
</g>
</g>
</svg>

</div>

</div>
<div>

**Undirected**
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="332pt" height="105pt"
 viewBox="0.00 0.00 332.00 105.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 101)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-101 328,-101 328,4 -4,4"/>

<g id="node1" class="node">
<title>a</title>
<ellipse fill="none" stroke="black" cx="117" cy="-41" rx="27" ry="18"/>
<text text-anchor="middle" x="117" y="-37.3" font-family="Times,serif" font-size="14.00">a</text>
</g>

<g id="node2" class="node">
<title>b</title>
<ellipse fill="none" stroke="black" cx="207" cy="-79" rx="27" ry="18"/>
<text text-anchor="middle" x="207" y="-75.3" font-family="Times,serif" font-size="14.00">b</text>
</g>

<g id="edge1" class="edge">
<title>a--b</title>
<path fill="none" stroke="black" d="M140.21,-50.59C153.55,-56.35 170.46,-63.65 183.8,-69.41"/>
</g>

<g id="node3" class="node">
<title>c</title>
<ellipse fill="none" stroke="black" cx="297" cy="-33" rx="27" ry="18"/>
<text text-anchor="middle" x="297" y="-29.3" font-family="Times,serif" font-size="14.00">c</text>
</g>

<g id="edge3" class="edge">
<title>a--c</title>
<path fill="none" stroke="black" d="M144.26,-39.82C178.02,-38.3 236.26,-35.69 269.92,-34.17"/>
</g>

<g id="edge2" class="edge">
<title>b--c</title>
<path fill="none" stroke="black" d="M228.85,-68.1C242.88,-60.77 261.3,-51.14 275.29,-43.82"/>
</g>

<g id="node4" class="node">
<title>d</title>
<ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">d</text>
</g>

<g id="edge5" class="edge">
<title>d--a</title>
<path fill="none" stroke="black" d="M52.51,-24.41C64.72,-27.6 79.43,-31.44 91.62,-34.63"/>
</g>

<g id="edge4" class="edge">
<title>d--c</title>
<path fill="none" stroke="black" d="M53.92,-15.95C65.03,-15.17 78.14,-14.38 90,-14 113.99,-13.23 120.05,-12.51 144,-14 188.72,-16.78 240.42,-24.13 270.54,-28.83"/>
</g>
</g>
</svg>

</div>

</div>
</div>

## Directed / Undirected
- Are city road maps directed or undirected?
- 
 What about social networks?

## Weighted / Unweighted
- A *weighted graph* has numerical values, called weights, assigned to each edge

</div>

## Weighted / Unweighted
- Can you think of situations where modeling something as a weighted graph could be useful?
- 
 Road networks
    + Speed limits and/or distances as weights
- 
 Piping networks
    + Flow capacities/rates as weights
- 
 Power line networks
    + Edges weighted by the cost to connect two nodes

## Simple / Non-Simple
- If a graph supports self-loops and/or duplicate edges it is called **non-simple**
- Otherwise they are called **simple**

**Simple**
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="332pt" height="105pt"
 viewBox="0.00 0.00 332.00 105.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 101)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-101 328,-101 328,4 -4,4"/>

<g id="node1" class="node">
<title>a</title>
<ellipse fill="none" stroke="black" cx="117" cy="-41" rx="27" ry="18"/>
<text text-anchor="middle" x="117" y="-37.3" font-family="Times,serif" font-size="14.00">a</text>
</g>

<g id="node2" class="node">
<title>b</title>
<ellipse fill="none" stroke="black" cx="207" cy="-79" rx="27" ry="18"/>
<text text-anchor="middle" x="207" y="-75.3" font-family="Times,serif" font-size="14.00">b</text>
</g>

<g id="edge1" class="edge">
<title>a--b</title>
<path fill="none" stroke="black" d="M140.21,-50.59C153.55,-56.35 170.46,-63.65 183.8,-69.41"/>
</g>

<g id="node3" class="node">
<title>c</title>
<ellipse fill="none" stroke="black" cx="297" cy="-33" rx="27" ry="18"/>
<text text-anchor="middle" x="297" y="-29.3" font-family="Times,serif" font-size="14.00">c</text>
</g>

<g id="edge3" class="edge">
<title>a--c</title>
<path fill="none" stroke="black" d="M144.26,-39.82C178.02,-38.3 236.26,-35.69 269.92,-34.17"/>
</g>

<g id="edge2" class="edge">
<title>b--c</title>
<path fill="none" stroke="black" d="M228.85,-68.1C242.88,-60.77 261.3,-51.14 275.29,-43.82"/>
</g>

<g id="node4" class="node">
<title>d</title>
<ellipse fill="none" stroke="black" cx="27" cy="-18" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-14.3" font-family="Times,serif" font-size="14.00">d</text>
</g>

<g id="edge5" class="edge">
<title>d--a</title>
<path fill="none" stroke="black" d="M52.51,-24.41C64.72,-27.6 79.43,-31.44 91.62,-34.63"/>
</g>

<g id="edge4" class="edge">
<title>d--c</title>
<path fill="none" stroke="black" d="M53.92,-15.95C65.03,-15.17 78.14,-14.38 90,-14 113.99,-13.23 120.05,-12.51 144,-14 188.72,-16.78 240.42,-24.13 270.54,-28.83"/>
</g>
</g>
</svg>

</div>

</div>
<div>

**Non-Simple**
<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="332pt" height="96pt"
 viewBox="0.00 0.00 332.00 96.44" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 92.44)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-92.44 328,-92.44 328,4 -4,4"/>

<g id="node1" class="node">
<title>a</title>
<ellipse fill="none" stroke="black" cx="117" cy="-32.44" rx="27" ry="18"/>
<text text-anchor="middle" x="117" y="-28.74" font-family="Times,serif" font-size="14.00">a</text>
</g>

<g id="edge7" class="edge">
<title>a--a</title>
<path fill="none" stroke="black" d="M101.77,-47.61C97.16,-58.11 102.23,-68.44 117,-68.44 131.77,-68.44 136.84,-58.11 132.23,-47.61"/>
</g>

<g id="node2" class="node">
<title>b</title>
<ellipse fill="none" stroke="black" cx="207" cy="-70.44" rx="27" ry="18"/>
<text text-anchor="middle" x="207" y="-66.74" font-family="Times,serif" font-size="14.00">b</text>
</g>

<g id="edge1" class="edge">
<title>a--b</title>
<path fill="none" stroke="black" d="M140.21,-42.03C153.55,-47.79 170.46,-55.1 183.8,-60.86"/>
</g>

<g id="node3" class="node">
<title>c</title>
<ellipse fill="none" stroke="black" cx="297" cy="-24.44" rx="27" ry="18"/>
<text text-anchor="middle" x="297" y="-20.74" font-family="Times,serif" font-size="14.00">c</text>
</g>

<g id="edge3" class="edge">
<title>a--c</title>
<path fill="none" stroke="black" d="M144.26,-31.26C178.02,-29.75 236.26,-27.13 269.92,-25.62"/>
</g>

<g id="edge2" class="edge">
<title>b--c</title>
<path fill="none" stroke="black" d="M228.85,-59.54C242.88,-52.21 261.3,-42.58 275.29,-35.27"/>
</g>

<g id="edge8" class="edge">
<title>c--c</title>
<path fill="none" stroke="black" d="M281.77,-39.61C277.16,-50.11 282.23,-60.44 297,-60.44 311.77,-60.44 316.84,-50.11 312.23,-39.61"/>
</g>

<g id="node4" class="node">
<title>d</title>
<ellipse fill="none" stroke="black" cx="27" cy="-32.44" rx="27" ry="18"/>
<text text-anchor="middle" x="27" y="-28.74" font-family="Times,serif" font-size="14.00">d</text>
</g>

<g id="edge5" class="edge">
<title>d--a</title>
<path fill="none" stroke="black" d="M52.51,-26.32C64.62,-25.49 79.19,-25.49 91.31,-26.31"/>
</g>

<g id="edge6" class="edge">
<title>d--a</title>
<path fill="none" stroke="black" d="M52.51,-38.57C64.62,-39.4 79.19,-39.4 91.31,-38.58"/>
</g>

<g id="edge4" class="edge">
<title>d--c</title>
<path fill="none" stroke="black" d="M48.24,-21.1C60.03,-15.15 75.4,-8.48 90,-5.44 154.87,8.07 233.24,-7.77 271.95,-17.66"/>
</g>
</g>
</svg>

</div>

</div>
</div>

## Sparse / Dense
- If I have a simple graph with $n$ vertices, what is the maximum number of edges possible?
    + 
 ${n \choose 2} = \frac{n(n-1)}{2}$
- 
 A **dense** graph has many edges, usually $\Omega(n^2)$
- 
 A **sparse** graph has few edges, usually $O(n)$

## Sparse / Dense

![Sparse and dense graphs](https://www.researchgate.net/profile/Atiye-Alaeddini/publication/305869701/figure/fig1/AS:393265800073216@1470773281885/Two-different-graph-topologies-of-a-network-of-15-nodes-a-dense-and-b-sparse.png)

## Sparse / Dense
- Is a road network sparse or dense?
     + 
 Sparse, because intersections usually have $O(1)$ connections
- 
 What about social networks?
    + 
 Also sparse
- 
 Can you think of an example of a **dense** graph?

## Cyclic / Acyclic
- An **acyclic** graph does not contain any cycles
    + Trees are undirected acyclic graphs
    + Directed acyclic graphs are called **DAG**s

</div>

# Social Networks

## The Friendship Graph
- Consider a graph where the vertices are people, and there is an edge between two people if and only if they are friends
    ![Harry Potter Friendship](../../assets/images/hp-friendship.png)
- 
 What questions can we ask about such a graph?

## Is friendship directed?
- Is a friendship graph directed or undirected?
    + 
 Hopefully undirected! If you are my friend then I hope that I am also your friend!
- 
 The "heard of" graph would be directed because many famous people have never heard of me

## Is there a path between us?
- Suppose I have a graph of actors/actresses where an edge exists between two people if they've starred in a movie together
- 
 What is the length of the shortest path between someone and Kevin Bacon?
- 
 A **path** between two vertices is a sequence of vertices that connects one to the other

## Six Degrees of Kevin Bacon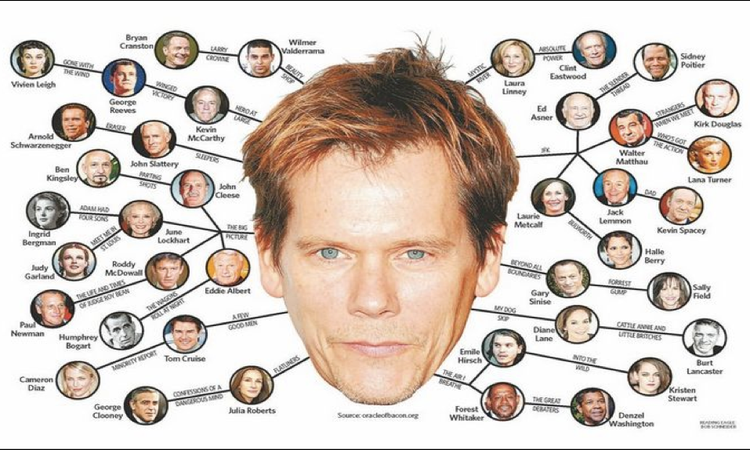
![Kevin Bacon](https://images.squarespace-cdn.com/content/v1/5a8d040564b05f9d780ecc2f/1554157278547-CG0BXDCS4ELRM4PWIQVA/image-asset.png?format=750w)

## Erdős Number
- Suppose I have a graph of all published scientists where two scientists share an edge if they have published a paper together
- 
 A person's **Erdős number** is the length of the shortest path between them and the Hungarian mathematician Paul Erdős
- 
 My Erdős number is 3

## Who has the most friends?
- The **degree** of a vertex is the number of edges connected to it
- 
 In directed graphs, each vertex has an **in-degree** and an **out-degree** to keep track of the asymmetry

## What is the largest clique?
- A social clique is a group of mutual friends who all hang out together
- 
 In a graph, a clique is a fully connected subgraph
- 
 Cliques are as dense as possible

# Implementing Graphs

## Implementing Graphs
- There are two main approaches to implementing a graph $G= (V,E)$ with $n$ vertices

## Adjacency Matrix
- We represent $G$ as a $n\times n$ matrix $M$, where $M[i,j]=1$ if $(i,j)$ is an edge and 0 if it isn't
- 
 This consumes $\Theta(n^2)$ space
- 
 Efficient, but wastes a lot of space for sparse graphs

## Adjacency List
- Alternatively we can represent $G$ in a linked way
    ```java
    class Vertex<V> {
        V data;
        List<Vertex<V>> neighbors;
    }
    ```
- 
 Each vertex stores a list of its adjacent vertices
- 
 We can keep track of the vertices in an array
- 
 To test if edge $(i,j)$ is in the graph, we need to iterate over $V[i].neighbors$ to see if it contains $j$

## Adjacency Lists/Matrices Comparison
- Which implementation strategy is more efficient for the following operations?

---

1. Testing if $(x,y)$ is in a graph
    - 
 Adjacency matrix ($O(1)$ instead of $O(n)$)
2. 
 Finding the degree of vertex $x$
    - 
 Adjacency list ($O(1)$ instead of $O(n)$)
3. 
 Memory usage on sparse graphs
    - 
 Adjacency list ($O(n+m)$ instead of $O(n^2)$)

## Adjacency List

4. Memory usage on dense graphs
    - 
 Adjacency matrix (a small win)
5. 
 Edge insertion or deletion
    - 
 Adjacency matrix ($O(1)$)
6. 
 Faster to traverse the graph
    - 
 Adjacency list ($O(n+m)$ instead of $O(n^2)$)

---

- 
 An **adjacency list** is best for most applications