reveal.js

# Exam Debrief
## and Maybe Graph Traversals

---

CS 137 // 2021-10-20

## Administrivia
- Exam 1 and a few daily exercises are graded and will be released immediately after class
- 
 Note that DE's are graded on a "GPA" scale
- 
 Adding +3 to everyone's exam due to wording issues on my part (mostly on problem 1b and 3)
- 
 For those with low scores, decided to calculate final grades as the maximum of two grading scales:
    1. 
 Midterm 1 / Final Exam as 20%/20%
    2. 
 Midterm 1 / Final Exam as 0%/40%

# Exam Review

## Assignment 2
- To help cement the concepts thus far in the course, I removed the next few daily exercises and released an assignment
- 
 The assignment is a deeper investigation into possible solutions to the last problem on the exam

# Questions
## ...about anything?

# Maze Solving

![Maze](https://d18l82el6cdm1i.cloudfront.net/image_optimizer/54429cab5dc05daafae44df6aae405409f240684.gif)

## Mazes are Just Graphs
- Note that a maze can be modeled as a graph
- 
 Every "room" is a vertex and every "door" is an edge
- 
 Thus, maze solving is equivalent to searching through the paths of a graph

# Graphs Traversals

## Graph Definition
- Recall that a **graph** is a linked data structure $G = (V,E)$  where:
    1. $V$ is a set of **vertices**
    2. $E$ is a set of **edges**
- 
 Graphs come in a variety of flavors
    + 
 Directed/undirected
    + 
 Weighted/unweighted
    + 
 Cyclic/acyclic

## Graph Definition

</div>

---

- $V = \\{a, b, c, d, e\\}$
- $E = \\{(a,b),(b,c),(a,c),(d,c),(c,e),(e,a)\\}$

## Graph Adjacency List

</div>

```py
# Represents a graph as a dictionary (hashtable) that maps
# vertices to a list of neighbors (i.e. adjacency list)
test_graph = {
    "a" : ["b","c"],
    "b" : ["c"],
    "d" : ["c"],
    "c" : ["e"],
    "e" : ["a"]
}
```

```py
# gets the neighbors of "a"
test_graph["a"]
```

## Graph Traversals
- Two common approaches for graph traversals:
    1. Depth-first search
    2. Breadth-first search
- 
 Similar to our maze solving algorithms, both approaches rely on tracking which vertices have already been visited

# Depth-First Search (DFS)

## Depth-First Search
- Core idea:
    + Maintain a **set** of vertices we've seen already
    + Maintain a **stack** of vertices we've discovered but haven't processed yet
    + 
 Repeatedly pop a vertex off the stack, push each unvisited neighbor to the stack and seen vertices

## DFS Visualization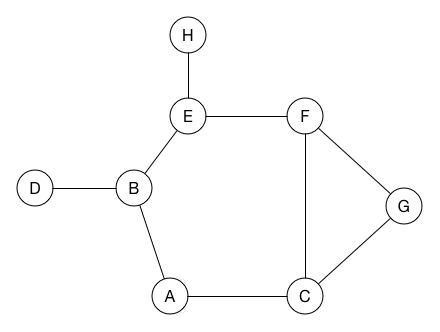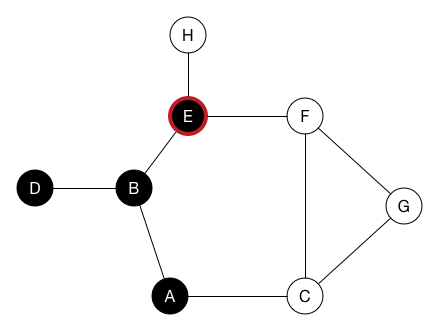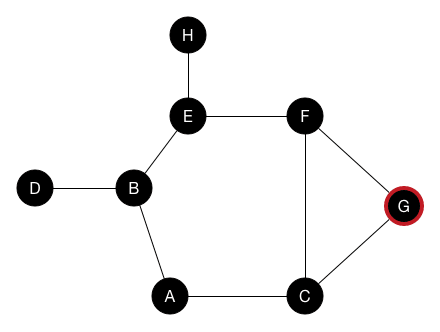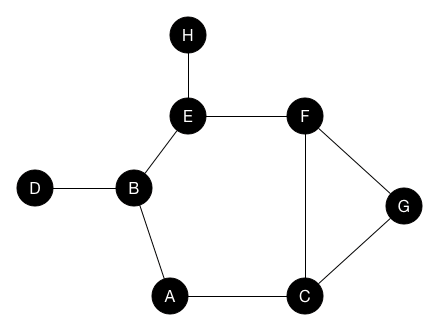

![DFS Visualization](https://aquarchitect.github.io/swift-algorithm-club/Depth-First%20Search/Images/AnimatedExample.gif)

## DFS Pseudocode

```text
dfs(g, start)
  Initialize set D = {start}
  Initialize stack S = (start)
  While S is not empty
    Let u = S.pop()
    Process the vertex u
    For each vertex, v, neighboring u
      If v is not in D
        Add v to D
        Push v to S
```

## DFS Implementation

```py
def dfs(g, start):
    discovered = {start}
    stack = [start]
    while len(stack) > 0:
        u = stack.pop()
        print(u)
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                stack.append(v)
```

## Using DFS to Solve Problems
- Many graph problems reduce to a traversal like DFS
- 
 How can we use DFS to solve mazes?

## Keeping Track of Paths
- It is possible to modify DFS in order to remember the path taken from the starting vertex
- 
 Need to remember the **parent** of discovered vertices

```py[2,12]
def dfs(g, start):
    parents = {start : None}
    discovered = {start}
    stack = [start]
    while len(stack) > 0:
        u = stack.pop()
        print(u)
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                stack.append(v)
                parents[v] = u
```

## Reconstructing Path
- Given `parents`, how can we reconstruct the path from `start` to a target vertex `end`?

```py
def construct_path(parents, start, end):
    if end not in parents: # end isn't reachable
        return None
    elif start == end:
        return [start]
    else:
        prev = parents[end]
        path = construct_path(parents, start, prev)
        path.append(end)
        return path
```

## Solving a Maze
- We now have what we need to solve general mazes:

```py
def solve_maze(g, start, end):
    parents = {start : None}
    discovered = {start}
    stack = [start]
    while len(stack) > 0:
        u = stack.pop()
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                stack.append(v)
                parents[v] = u
    return construct_path(parents, start, end)
```