reveal.js

# Graph Traversals
## and Topological Sort
---

CS 137 // 2021-10-25

## Administrivia
- Assignment 2 is due on Wednesday
    + Let me know if you need an extension
- 
 DE6 returned on Gradescope
- 
 If you haven't already, please fill out the [midterm evaluation questionnaire](https://docs.google.com/forms/d/e/1FAIpQLSeWe6Nd0ndk-XsfXjH9a3_B9lsRtY6yQFUtPltsXj8n2OoirA/viewform?usp=sf_link)
    + Need to be signed into Google with your Drake email address

# Questions
## ...about anything?

# Maze Solving

## Maze Solving

![Maze](https://d18l82el6cdm1i.cloudfront.net/image_optimizer/54429cab5dc05daafae44df6aae405409f240684.gif)

## Mazes are Just Graphs
- Note that a maze can be modeled as a graph
- Every "room" is a vertex and every "door" is an edge
- Thus, maze solving is equivalent to searching through the paths of a graph

## Graph Adjacency List

</div>

```py
# Represents a graph as a dictionary (hashtable) that maps
# vertices to a list of neighbors (i.e. adjacency list)
test_graph = {
    "a" : ["b","c"],
    "b" : ["c"],
    "d" : ["c"],
    "c" : ["e"],
    "e" : ["a"]
}

test_graph["a"] # gets the neighbors of "a"
```

# Depth-First Search (DFS)

## Depth-First Search
- Core idea:
    + Maintain a **set** of vertices we've seen already
    + Maintain a **stack** of vertices we've discovered but haven't processed yet
    + Repeatedly pop a vertex off the stack, push each unvisited neighbor to the stack and seen vertices

## DFS Visualization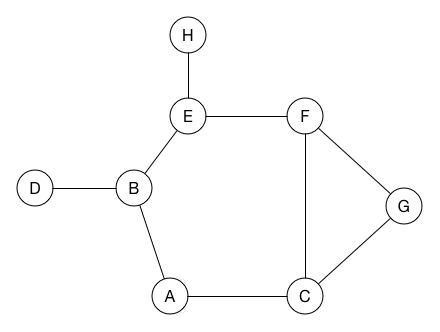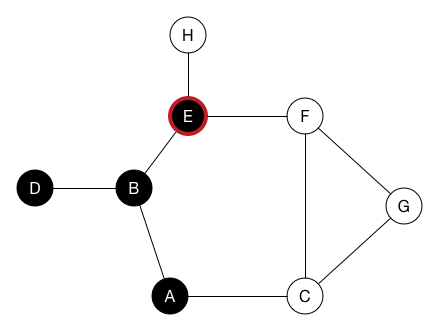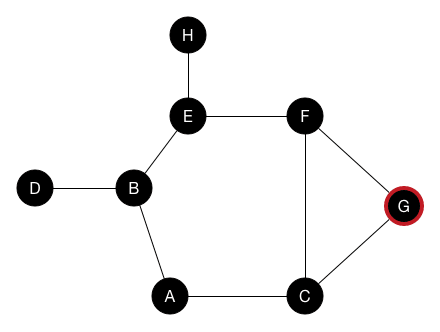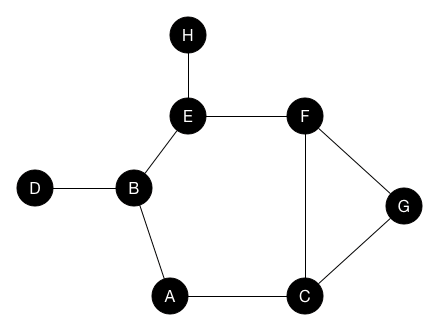

![DFS Visualization](https://aquarchitect.github.io/swift-algorithm-club/Depth-First%20Search/Images/AnimatedExample.gif)

## DFS Pseudocode

```text
dfs(g, start)
  Initialize set D = {start}
  Initialize stack S = (start)
  While S is not empty
    Let u = S.pop()
    Process the vertex u
    For each vertex, v, neighboring u
      If v is not in D
        Add v to D
        Push v to S
```

## DFS Implementation

```py
def dfs(g, start):
    discovered = {start}
    stack = [start]
    while len(stack) > 0:
        u = stack.pop()
        print(u)
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                stack.append(v)
```

- 
 Given a graph with $n$ vertices and $m$ edges, what is the runtime complexity of DFS?
    - 
 $O(n + m)$, (each vertex/edge is touched once)
    - 
 This is the "linear time" for graphs

## Using DFS to Solve Problems
- Many graph problems reduce to a traversal like DFS
- 
 How can we use DFS to solve mazes?

## Keeping Track of Paths
- It is possible to modify DFS in order to remember the path taken from the starting vertex
- 
 Need to remember the **parent** of discovered vertices

```py[2,12]
def dfs(g, start):
    parents = {start : None}
    discovered = {start}
    stack = [start]
    while len(stack) > 0:
        u = stack.pop()
        print(u)
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                stack.append(v)
                parents[v] = u
```

## Reconstructing Path
- Given `parents`, how can we reconstruct the path from `start` to a target vertex `end`?

```py
def construct_path(parents, start, end):
    if end not in parents: # end isn't reachable
        return None
    elif start == end:
        return [start]
    else:
        prev = parents[end]
        path = construct_path(parents, start, prev)
        path.append(end)
        return path
```

## Solving a Maze
- We now have what we need to solve general mazes:
    ```py
    def solve_maze(g, start, end):
        parents = {start : None}
        discovered = {start}
        stack = [start]
        while len(stack) > 0:
            u = stack.pop()
            for v in g[u]:
                if v not in discovered:
                    discovered.add(v)
                    stack.append(v)
                    parents[v] = u
        return construct_path(parents, start, end)
    ```
- 
 Does this algorithm always return the shortest path?
    + 
 No. Will return first path found even if long

## Finding the Shortest Path
- For shortest path, we need another approach
- 
 Note that with DFS we always process the most recently discovered vertex
    + 
 This causes us to go "deep" down a path and only turn around when we find a dead end
- 
 What if we process the vertices in a different order?

![BFS Maze Solving](https://thumbs.gfycat.com/OptimalWelldocumentedAnaconda-max-1mb.gif)

# Breadth-First Search (BFS)

## Breadth-First Search (BFS)
- The core idea behind BFS is the same as DFS except we process the vertices in a different order
- 
 Instead of processing the last discovered vertex, we will process vertices in the order we find them
    + 
 Instead of a "last in first out" we want a "first in first out" ordering

## BFS Implementation

```py[1-12|5,12]
from collections import deque

def bfs(g, start):
    discovered = {start}
    queue = deque(discovered)
    while len(queue) > 0:
        u = queue.pop()
        print(u)
        for v in g[u]:
            if v not in discovered:
                discovered.add(v)
                queue.appendleft(v)
```

## DFS and BFS Visualization

![BFS DFS Comparison](https://miro.medium.com/max/1280/1*GT9oSo0agIeIj6nTg3jFEA.gif)

## Exercise
- BFS can be used to find the shortest path **from** a vertex $u$ to every other reachable vertex in the graph
- 
 Suppose we want to do something similar:
    + Find the shortest path **to** a vertex $u$ from every other vertex in the graph
- 
 With your table, come up with an algorithm for this
    + No need to write code---just the idea

## Exercise
- A directed graph is **strongly connected** if for every pair of vertices, $u,v$, there is a path starting at $u$ and ending at $v$
- 
 With your table, come up with an algorithm for this
    + No need to write code---just the idea

# Topological Sort

## Prerequisite Graphs
- An issue you might be familiar with is writing a schedule to take all the CS requirements in some particular order (four year plan)

---

<div class='jekyll-diagrams diagrams graphviz'>
  

<svg width="486pt" height="268pt"
 viewBox="0.00 0.00 486.00 268.00" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink">
<g id="graph0" class="graph" transform="scale(1 1) rotate(0) translate(4 264)">
<title>%3</title>
<polygon fill="white" stroke="transparent" points="-4,4 -4,-264 482,-264 482,4 -4,4"/>

<g id="node1" class="node">
<title>cs147</title>
<polygon fill="none" stroke="black" points="166,-112 86,-112 86,-74 166,-74 166,-112"/>
<text text-anchor="middle" x="126" y="-96.8" font-family="Times,serif" font-size="14.00">CS 147</text>
<text text-anchor="middle" x="126" y="-81.8" font-family="Times,serif" font-size="14.00">Graphics</text>
</g>

<g id="node2" class="node">
<title>cs167</title>
<polygon fill="none" stroke="black" points="286,-186 176,-186 176,-148 286,-148 286,-186"/>
<text text-anchor="middle" x="231" y="-170.8" font-family="Times,serif" font-size="14.00">CS 167</text>
<text text-anchor="middle" x="231" y="-155.8" font-family="Times,serif" font-size="14.00">Mach. Learn.</text>
</g>

<g id="node3" class="node">
<title>cs178</title>
<polygon fill="none" stroke="black" points="252,-112 184,-112 184,-74 252,-74 252,-112"/>
<text text-anchor="middle" x="218" y="-96.8" font-family="Times,serif" font-size="14.00">CS 178</text>
<text text-anchor="middle" x="218" y="-81.8" font-family="Times,serif" font-size="14.00">Cloud</text>
</g>

<g id="node4" class="node">
<title>cs65</title>
<polygon fill="lightblue" stroke="lightblue" points="260.5,-260 201.5,-260 201.5,-222 260.5,-222 260.5,-260"/>
<text text-anchor="middle" x="231" y="-244.8" font-family="Times,serif" font-size="14.00">CS 65</text>
<text text-anchor="middle" x="231" y="-229.8" font-family="Times,serif" font-size="14.00">CS I</text>
</g>

<g id="edge1" class="edge">
<title>cs65->cs167</title>
<path fill="none" stroke="black" d="M231,-221.83C231,-214.13 231,-204.97 231,-196.42"/>
<polygon fill="black" stroke="black" points="234.5,-196.41 231,-186.41 227.5,-196.41 234.5,-196.41"/>
</g>

<g id="node5" class="node">
<title>cs66</title>
<polygon fill="lightblue" stroke="lightblue" points="157.5,-186 98.5,-186 98.5,-148 157.5,-148 157.5,-186"/>
<text text-anchor="middle" x="128" y="-170.8" font-family="Times,serif" font-size="14.00">CS 66</text>
<text text-anchor="middle" x="128" y="-155.8" font-family="Times,serif" font-size="14.00">CS II</text>
</g>

<g id="edge2" class="edge">
<title>cs65->cs66</title>
<path fill="none" stroke="black" d="M205.01,-221.83C192.08,-212.79 176.28,-201.75 162.36,-192.02"/>
<polygon fill="black" stroke="black" points="164.18,-189.02 153.98,-186.16 160.17,-194.76 164.18,-189.02"/>
</g>

<g id="node13" class="node">
<title>cs139</title>
<polygon fill="lightseagreen" stroke="lightseagreen" points="372,-186 304,-186 304,-148 372,-148 372,-186"/>
<text text-anchor="middle" x="338" y="-170.8" font-family="Times,serif" font-size="14.00">CS 139</text>
<text text-anchor="middle" x="338" y="-155.8" font-family="Times,serif" font-size="14.00">Theory</text>
</g>

<g id="edge3" class="edge">
<title>cs65->cs139</title>
<path fill="none" stroke="black" d="M258,-221.83C271.43,-212.79 287.85,-201.75 302.3,-192.02"/>
<polygon fill="black" stroke="black" points="304.67,-194.65 311.01,-186.16 300.76,-188.84 304.67,-194.65"/>
</g>

<g id="edge4" class="edge">
<title>cs66->cs147</title>
<path fill="none" stroke="black" d="M127.5,-147.83C127.28,-140.13 127.03,-130.97 126.79,-122.42"/>
<polygon fill="black" stroke="black" points="130.29,-122.31 126.51,-112.41 123.29,-122.51 130.29,-122.31"/>
</g>

<g id="edge5" class="edge">
<title>cs66->cs178</title>
<path fill="none" stroke="black" d="M150.71,-147.83C161.8,-138.96 175.3,-128.16 187.29,-118.57"/>
<polygon fill="black" stroke="black" points="189.67,-121.14 195.3,-112.16 185.3,-115.68 189.67,-121.14"/>
</g>

<g id="node6" class="node">
<title>cs146</title>
<polygon fill="lightblue" stroke="lightblue" points="329.5,-112 270.5,-112 270.5,-74 329.5,-74 329.5,-112"/>
<text text-anchor="middle" x="300" y="-96.8" font-family="Times,serif" font-size="14.00">CS 67</text>
<text text-anchor="middle" x="300" y="-81.8" font-family="Times,serif" font-size="14.00">CS III</text>
</g>

<g id="edge6" class="edge">
<title>cs66->cs146</title>
<path fill="none" stroke="black" d="M157.72,-152.04C160.84,-150.64 163.98,-149.27 167,-148 208.22,-130.62 219.78,-129.38 261,-112 261.09,-111.96 261.19,-111.92 261.28,-111.88"/>
<polygon fill="black" stroke="black" points="262.51,-115.16 270.28,-107.96 259.71,-108.75 262.51,-115.16"/>
</g>

<g id="node7" class="node">
<title>cs130</title>
<polygon fill="lightblue" stroke="lightblue" points="68,-112 0,-112 0,-74 68,-74 68,-112"/>
<text text-anchor="middle" x="34" y="-96.8" font-family="Times,serif" font-size="14.00">CS 130</text>
<text text-anchor="middle" x="34" y="-81.8" font-family="Times,serif" font-size="14.00">Org I</text>
</g>

<g id="edge7" class="edge">
<title>cs66->cs130</title>
<path fill="none" stroke="black" d="M104.28,-147.83C92.59,-138.88 78.33,-127.96 65.72,-118.3"/>
<polygon fill="black" stroke="black" points="67.78,-115.47 57.71,-112.16 63.52,-121.02 67.78,-115.47"/>
</g>

<g id="node8" class="node">
<title>cs135</title>
<polygon fill="lightblue" stroke="lightblue" points="334,-38 266,-38 266,0 334,0 334,-38"/>
<text text-anchor="middle" x="300" y="-22.8" font-family="Times,serif" font-size="14.00">CS 135</text>
<text text-anchor="middle" x="300" y="-7.8" font-family="Times,serif" font-size="14.00">PL</text>
</g>

<g id="edge8" class="edge">
<title>cs146->cs135</title>
<path fill="none" stroke="black" d="M300,-73.83C300,-66.13 300,-56.97 300,-48.42"/>
<polygon fill="black" stroke="black" points="303.5,-48.41 300,-38.41 296.5,-48.41 303.5,-48.41"/>
</g>

<g id="node9" class="node">
<title>cs137</title>
<polygon fill="lightblue" stroke="lightblue" points="447.5,-38 352.5,-38 352.5,0 447.5,0 447.5,-38"/>
<text text-anchor="middle" x="400" y="-22.8" font-family="Times,serif" font-size="14.00">CS 137</text>
<text text-anchor="middle" x="400" y="-7.8" font-family="Times,serif" font-size="14.00">Algorithms</text>
</g>

<g id="edge9" class="edge">
<title>cs146->cs137</title>
<path fill="none" stroke="black" d="M325.23,-73.83C337.79,-64.79 353.13,-53.75 366.64,-44.02"/>
<polygon fill="black" stroke="black" points="368.7,-46.85 374.77,-38.16 364.61,-41.17 368.7,-46.85"/>
</g>

<g id="node12" class="node">
<title>cs188</title>
<polygon fill="lightblue" stroke="lightblue" points="248,-38 180,-38 180,0 248,0 248,-38"/>
<text text-anchor="middle" x="214" y="-22.8" font-family="Times,serif" font-size="14.00">CS 188</text>
<text text-anchor="middle" x="214" y="-7.8" font-family="Times,serif" font-size="14.00">SE</text>
</g>

<g id="edge10" class="edge">
<title>cs146->cs188</title>
<path fill="none" stroke="black" d="M278.3,-73.83C267.81,-65.05 255.05,-54.37 243.68,-44.85"/>
<polygon fill="black" stroke="black" points="245.61,-41.9 235.69,-38.16 241.12,-47.27 245.61,-41.9"/>
</g>

<g id="node10" class="node">
<title>math54</title>
<polygon fill="lightblue" stroke="lightblue" points="397.5,-260 278.5,-260 278.5,-222 397.5,-222 397.5,-260"/>
<text text-anchor="middle" x="338" y="-244.8" font-family="Times,serif" font-size="14.00">MATH 54</text>
<text text-anchor="middle" x="338" y="-229.8" font-family="Times,serif" font-size="14.00">Discrete Math</text>
</g>

<g id="edge11" class="edge">
<title>math54->cs167</title>
<path fill="none" stroke="black" d="M311,-221.83C297.57,-212.79 281.15,-201.75 266.7,-192.02"/>
<polygon fill="black" stroke="black" points="268.24,-188.84 257.99,-186.16 264.33,-194.65 268.24,-188.84"/>
</g>

<g id="edge12" class="edge">
<title>math54->cs137</title>
<path fill="none" stroke="black" d="M356.85,-221.72C365.7,-211.98 375.49,-199.28 381,-186 399.86,-140.55 402.06,-82.44 401.41,-48.41"/>
<polygon fill="black" stroke="black" points="404.9,-48.15 401.11,-38.25 397.91,-48.35 404.9,-48.15"/>
</g>

<g id="edge13" class="edge">
<title>math54->cs139</title>
<path fill="none" stroke="black" d="M338,-221.83C338,-214.13 338,-204.97 338,-196.42"/>
<polygon fill="black" stroke="black" points="341.5,-196.41 338,-186.41 334.5,-196.41 341.5,-196.41"/>
</g>

<g id="node11" class="node">
<title>cs83</title>
<polygon fill="lightblue" stroke="lightblue" points="478,-260 416,-260 416,-222 478,-222 478,-260"/>
<text text-anchor="middle" x="447" y="-244.8" font-family="Times,serif" font-size="14.00">CS 83</text>
<text text-anchor="middle" x="447" y="-229.8" font-family="Times,serif" font-size="14.00">Ethics</text>
</g>
</g>
</svg>

</div>

## Directed Acyclic Graphs
- A dependency graph like this is called a **directed acyclic graph** or **DAG** for short
- 
 Why doesn't it make sense for a dependency graph to have a cycle?
    + 
 Cyclical dependencies means some courses cannot be taken without skipping a prerequisite

## Exercise
- Write down a sensible ordering for a student to take the following courses

---

</div>

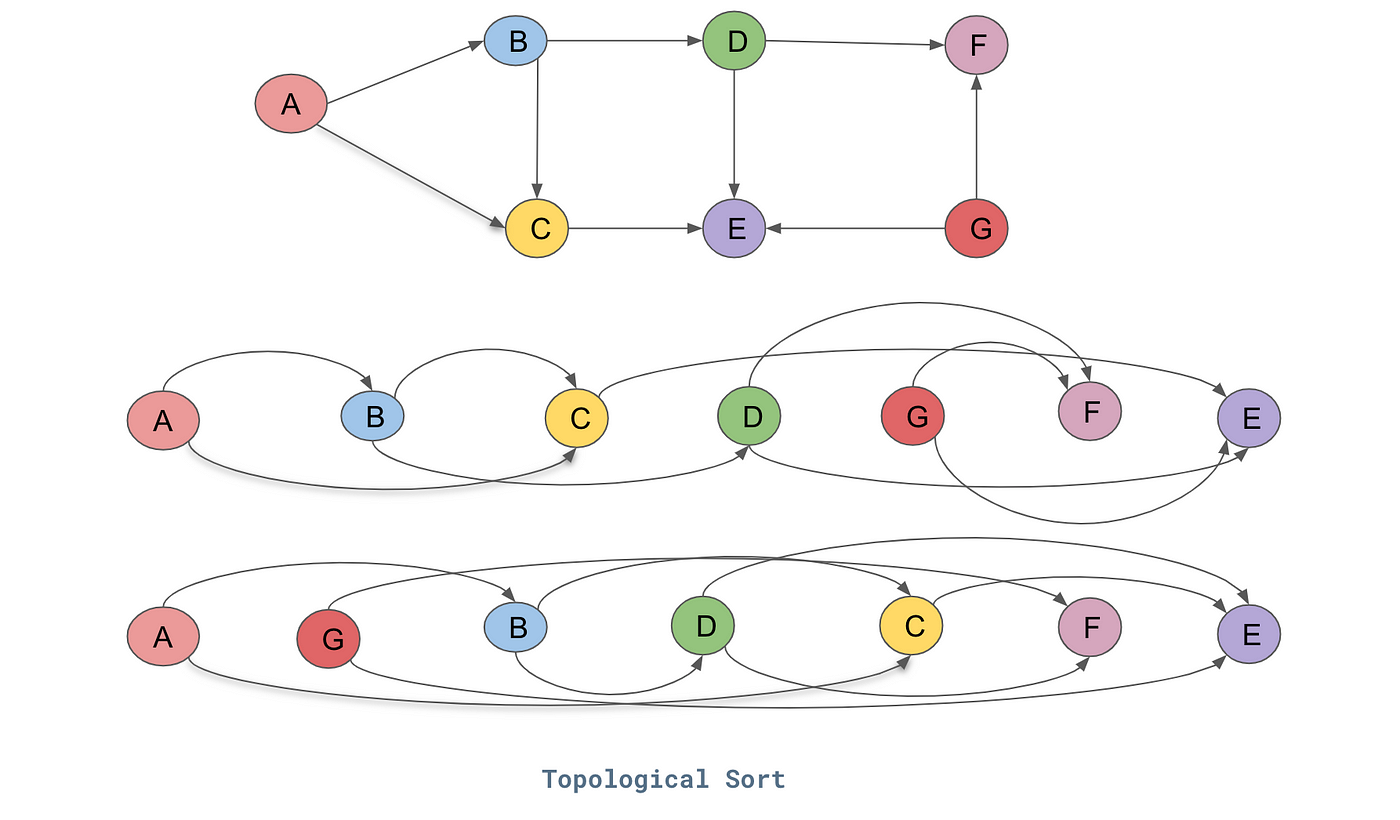## Topological Ordering
![Topological Ordering](https://miro.medium.com/max/1400/1*uMg_ojFXts2WZSjcZe4oRQ.png)

## Topological Sort
- An algorithm for finding a topological ordering is called a **topological sort**
- 
 Your process for composing a four-year plan is literally a topological sort
- 
 The core idea behind the topological sort algorithm is exactly the process you used to order the courses

## Topological Sort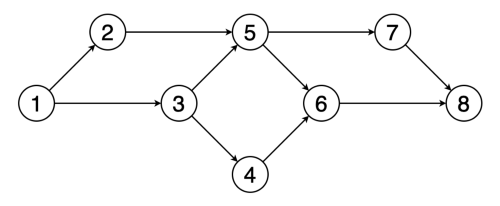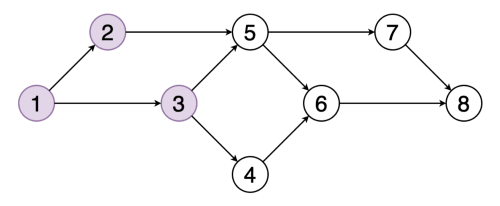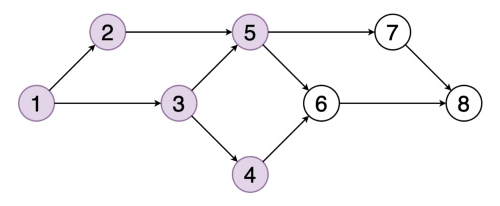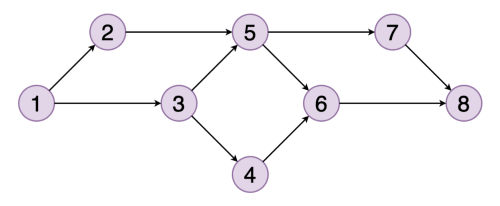

![Topological Sort](https://raw.githubusercontent.com/yousefwalid/CMP302-Summary/master/assets/graphs/topological.gif)

---

1. Pick a vertex with in-degree zero (no prerequisites) and add it to our output ordering
2. 
 Remove it from the graph
3. 
 Repeat until no vertices are left

## Calculating the In-Degrees of Vertices
```py
def in_degree(g):
    """Calculates the in-degree of all vertices"""
    degree = {u:0 for u in g}
    for u in g:
        for v in g[u]:
            degree[v] += 1
    return degree
```

## Topological Sort Implementation

```py
def toposort(g):
    degree = in_degree(g)
    ready = [u for u in degree if degree[u] == 0]
    output = []
    while len(ready) > 0:
        u = ready.pop()
        output.append(u)
        for v in g[u]:
            degree[v] -= 1
            if degree[v] == 0:
                ready.append(v)

return output

```