reveal.js

## Minimum Spanning Trees
# Continued
---

CS 137 // 2021-11-01

## Administrivia
-

# Questions
## ...about anything?

# Minimum Spanning Trees

## Weighted Graphs
- Recall that a *weighted graph* has numerical values, called weights, assigned to each edge

</div>

## Spanning Trees
- Given an undirected, connected, graph $G=(V,E)$, a **spanning tree** is a connected subgraph $T = (V,E')$ with $E'\subseteq E$ with no cycles

![Spanning Trees](/teaching/2021f/cs137/assets/images/msts.png)

## Minimum Spanning Tree

- **Input**: A connected, weighted, undirected graph $G = (V,E)$ with weights $w:E\rightarrow\mathbb{R}_{>0}$
- **Output**: a tree $T = (V,E')$ where $E'\subseteq E$ so that $\\sum_\{e\\in E'\} w(e)$ is minimized

## Minimum Spanning Trees
- Finding the **minimum spanning tree** (**MST**) is extremely useful for a lot of problems

![Minimum Spanning Tree](https://homes.luddy.indiana.edu/achauhan/Teaching/B403/LectureNotes/images/09-mst-intro.jpg)

# Prim's Algorithm

## Prim's Algorithm
- Prim's approach to find an MST is **greedy**
- 
 The main idea is to build up a partial MST and keep choosing the **cheapest** edge out of the tree that doesn't create a cycle

## Prim's Visualization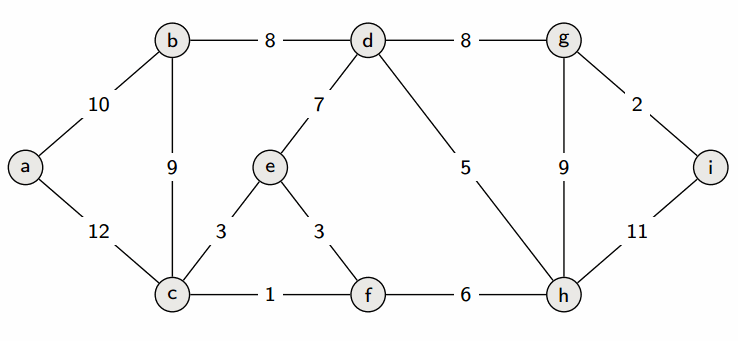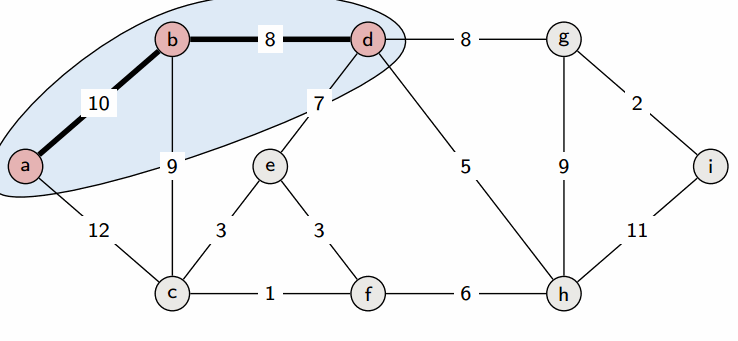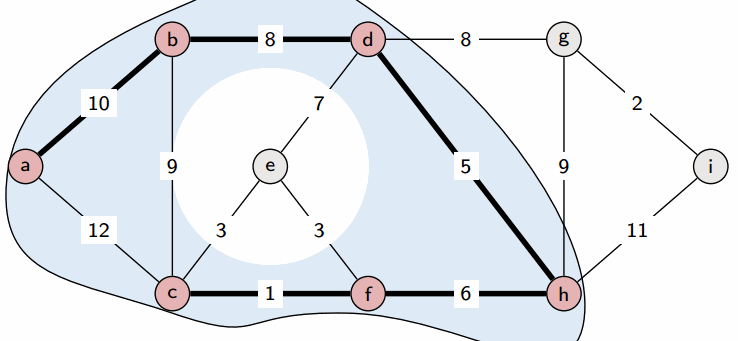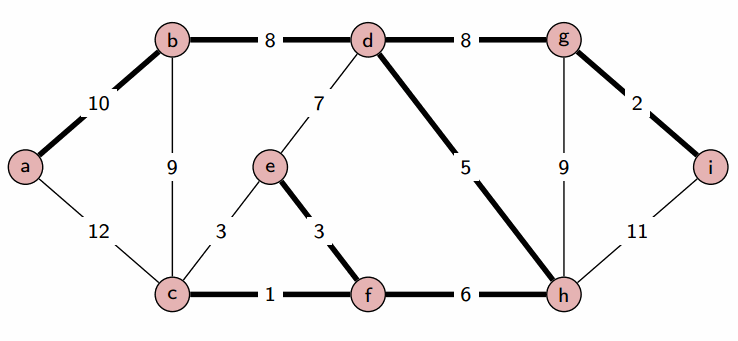

![Prim's Algorithm](https://kjaer.io/images/algorithms/prim.gif)

## Prim's Pseudocode

1. 
 Let $x\in V$ be an arbitrary vertex in $G = (V,E)$
2. 
 Set $S = \\{x\\}$ and $E' = \emptyset$
3. 
 While $S \ne V$, do the following:
    1. 
 Let $(u,v)\in E$ be the cheapest edge satisfying $u\in S$ and $v\not\in S$
    2. 
 Add $(u,v)$ to $E'$ and $v$ to $S$
4. 
 Return $T = (V,E')$

## Is Prim's Correct?
- 
 Since it is always adding a disconnected vertex to the blob, it will never create a cycle
    + 
 Thus, it definitely returns a spanning tree
- 
 Is the spanning tree *minimal* though?

## Proof by Contradiction
- Assume that it is possible for Prim's to return a sub-optimal MST
- 
 Let $G = (V,E)$ be a graph where Prim's fails
- 
 Since the algorithm returns a spanning tree that is not minimal, let $(x,y)$ be the first edge added by Prim's that differs from the MST

## Proof by Contradiction
![Prim's exchange argument](../../assets/images/prims-exchange.png)

- Since $(x,y)$ is not in the MST of $G$, there must be some other path from $x$ to $y$ in the MST
- 
 Let $(v_1, v_2)$ be the edge that connects the two subgraphs in the MST along this path

## Proof by Contradiction

![Prim's exchange argument](../../assets/images/prims-exchange.png)

- Since Prim's selected $(x, y)$ instead of $(v_1, v_2)$, exchanging this edge for $(x,y)$ yields a spanning tree of lesser weight
- 
 Thus, Prim's actually *did* return an MST!

## How fast is Prim's Algorithm?
- Depends on what data structure is used
- 
 If we do a linear search for the cheapest edge every time, the runtime is $O(nm)$
- 
 If we employ a min-heap data structure, it can be improved to $O(m\log m)$
- 
 With an even fancier data structure, it can be improved to $O(m + n\log n)$

# Kruskal's Algorithm

## Kruskal's Algorithm
1. Sort the edges of $G$ in increasing order of weight
2. For each edge $e$ in this order:
    1. Add $e$ to $T$ if it connects two components in $T$
3. Return $T$

## Kruskal's Algorithm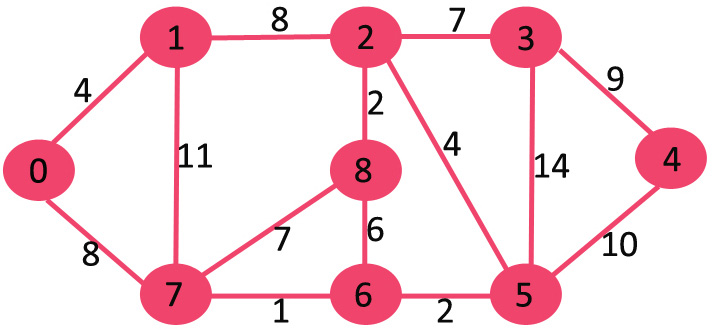
![Find an MST](https://www.geeksforgeeks.org/wp-content/uploads/Fig-11.jpg)

## Kruskal's Algorithm Visualization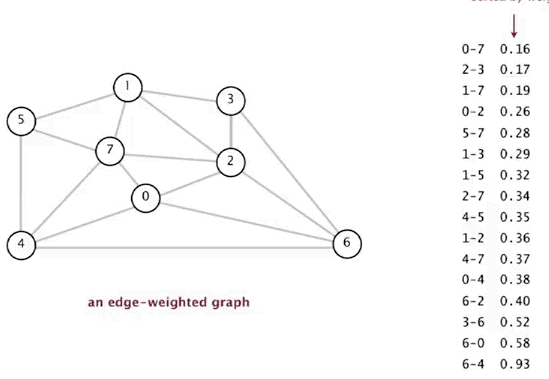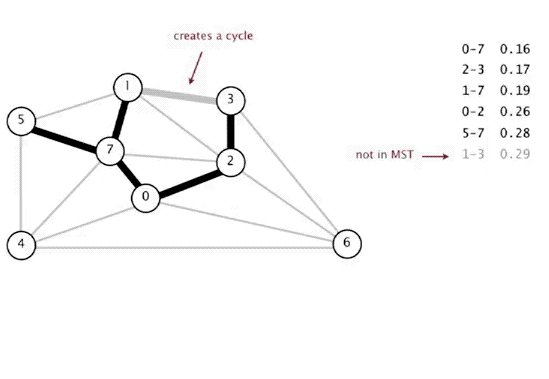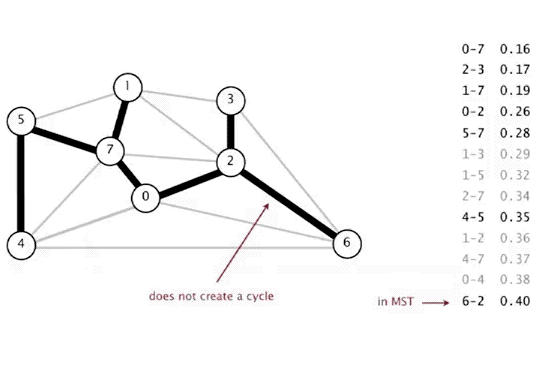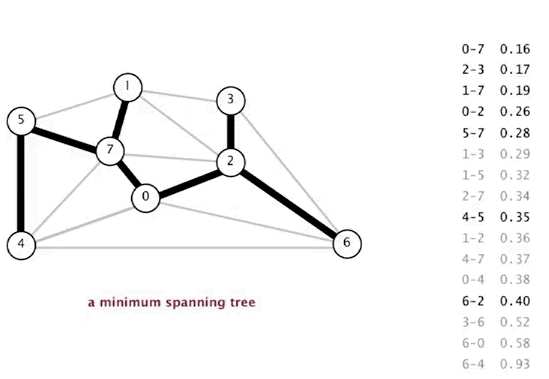

![Kruskal's Algorithm](https://techlarry.github.io/Algorithm/Princeton/figures/kruskals-algorithm_demo.gif)

## Is Kruskal's Correct?
- It keeps adding edges without creating a cycle, so it does produce a spanning tree with $n-1$ edges
- 
 Is it minimal though?

## Proof by Contradiction
- Assume that it is possible for Kruskal's to return a sub-optimal MST
- Let $G = (V,E)$ be a graph where Kruskal's fails
- Since the algorithm returns a spanning tree that is not minimal, let $(x,y)$ be the first edge added by Kruskal's that differs from the MST

## Proof by Contradiction
- If we add $(x,y)$ to the true MST of $G$ it creates a cycle between vertices $x$ and $y$
- 
 Now, if we delete the cheapest edge along the cycle we should minimize the cost
- 
 But the minimum cost edge in the cycle is $(x,y)$, otherwise Kruskal's would have selected it first
- 
 Thus, Kruskal's returns an MST after all!

## How Fast is Kruskal's?
1. Sort the edges of $G$ in increasing order of weight
2. For each edge $e$ in this order:
    1. Add $e$ to $T$ if it connects two components in $T$
3. Return $T$

---

- 
 Sorting edges takes $O(m\log m)$
- 
 Loop runs $m$ times
- 
 We could use BFS to check if two vertices are connected already, but that takes $O(n+m)$-time
    + 
 Can we do better?

# Union-Find

## Union-Find Data Structure
- What we need is a data structure that supports two operations:
    1. **Find(x)**: returns the component $x$ belongs to
    2. **Union(x,y)**: merges the components of $x$ and $y$
- 
 Ideally, each of these operations should take at most $O(\log n)$

## Union-Find Implementation
- **Idea:** Use a *forest*, i.e., collection of trees!
    + 
 Elements are leaves
    + 
 Roots are the "label" of the component that the element belongs to
    + 
 Merge labels by combining trees

![Union Find](https://upload.wikimedia.org/wikipedia/commons/thumb/a/a3/UnionFindKruskalDemo.gif/500px-UnionFindKruskalDemo.gif)

## Union-Find Runtime
- Both operations are $O(\log n)$ if we union by making the smaller tree a subchild of the taller tree
    + 
 Tree only gets taller when two subtrees are the same size
    + 
 Each operation requires starting from a leaf and finding the root

## Overall Runtime of Kruskal's
- Becomes $O(m\log n)$ because find/union operations run once per execution of the loop
- 
 Thus, Kruskal's is similar to Prim's in runtime