reveal.js

# Shortest Paths
---

CS 137 // 2021-11-03

## Administrivia
- Noyce Scholarship
- 
 Assignment 2 debrief

# Questions
## ...about anything?

# Greedy Algorithms

## Greedy Algorithms
- Recently we've looked at two algorithms to find a minimum spanning tree
- 
 Prim's algorithm chooses the **cheapest** edge that extends the connected subgraph
- 
 Kruskal's algorithm chooses the **cheapest** edge that connects two distinct components

## Greedy Algorithms

- Algorithms of this "best thing first" variety are called **greedy** algorithms
- 
 Greedy algorithms can be used to solve a wide variety of problems, but it doesn't work for all problems
    + 
 We will see a few later in the course

# Shortest Paths

## Unweighted Graphs
- We've already discussed an algorithm for finding the shortest path in **unweighted** graphs
    + What was the algorithm?
    + 
 We used **breath-first search** (**BFS**)
        ![BFS DFS Comparison](https://miro.medium.com/max/1280/1*GT9oSo0agIeIj6nTg3jFEA.gif)

## Weighted Graphs
- An important variation of shortest path is one for **weighted graphs**
- 
 **INPUT:**
    + Directed graph $G = (V,E)$
    + Start and destination vertices $s,t\in V$
    + Weights $w:E\\rightarrow\\mathbb{Z}_{\\ge 0}$
- 
 **OUTPUT:**
    + Length of the shortest path from $s$ to $t$
    + 
 "Length" means sum of edge weights along path

## Weighted Graphs
- Why will BFS not necessarily return the correct answer for weighted graphs?
    + Can you come up with a counterexample?
- 
 One theme of this course is to be **lazy** when possible
- 
 Is there a way we can modify a weighted graph $G$ so that BFS will return the correct answer?

## Edge Expansion
- **Idea**: "expand" the edges of the weighted graph

---

</div>

</div>
<div>

</div>

</div>
</div>

---

- 
 By expanding every edge like this, BFS returns the correct answer in $O(n + W)$-time
    + where $W = \sum_{e\in E} w(e)$
- 
 Can we do better?
    + 
 Absolutely!

## Finding Short Paths
- Think about how you normally find short paths
    + What is the shortest path from 0 to 4?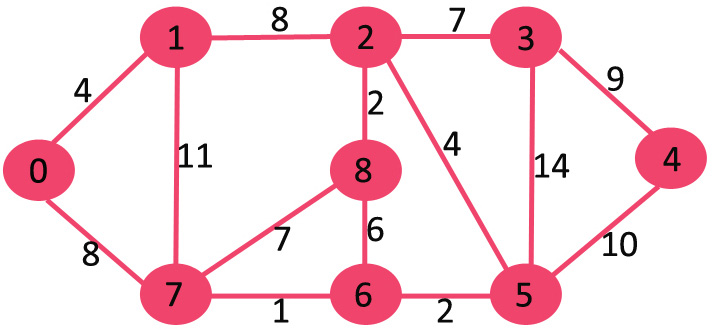

![Finding Short Paths](https://www.geeksforgeeks.org/wp-content/uploads/Fig-11.jpg)

# Dijkstra's Algorithm

## Dijkstra's Algorithm
- **Idea:** Greedily expand a set of nodes where the shortest distance from $s$ is known

## Dijkstra's Visualization

![Dijkstra's Visualization](https://upload.wikimedia.org/wikipedia/commons/5/57/Dijkstra_Animation.gif)

## Dijkstra's Pseudocode

1. 
 Set $D[s] = 0$ and $D[v] = +\infty$ for other vertices
2. 
 While at least one $D[v] = +\infty$:
    1. 
 Choose such a $v$ that is "closest" to $s$
        - 
 i.e., d = $w(u,v) + D[u]$ is minimal
    2. 
 If $d = +\infty$, then return $D$,<br>otherwise set $D[v] = d$
3. 
 Return $D$

# Worksheet

## Dijkstra's Runtime
- What is the runtime of Dijkstra's?
    + 
 Depends on the data structure used!
    + 
 $O(nm)$ if we do a traversal each loop
    + 
 $O(m\log n)$ if we use a min-heap

## Exercise:
- What if instead of the edges carrying the weights we have vertices carrying the weights instead?
- 
 Is there a way to "be lazy" and use normal Dijksta's algorithm?

## Exercise: Finding a Maximum Spanning Tree
- Suppose I want to find a spanning tree where the sum of the edge weights is *maximized* instead of minimized
- 
 Is there a way to "be lazy" and use normal Prim's or Kruskal's?

## Principle of Graph Problems
- Whenever possible, **build graphs**, not algorithms