reveal.js

# Searching and Recursion

---

CS 65 // 2021-04-20

## Administrivia
- Project proposal due Thursday

# Questions
## ...about anything?

# Searching

# Searching
- Suppose you have a **phonebook** in your hands
- How do you go about searching for a name?

## Formalizing the Problem
```py
def search(val, lst):
    """Finds the index of val in lst or -1 if not found

Parameters:
        val: an object
        lst: a list

Returns:
        index: an int

Postconditions:
        if lst contains val, then lst[index] == val
        otherwise index == -1
    """
```
- 
 How would you implement this function?

## Linear Search
```py
def search(val, lst):
    """Finds the index of val in lst or -1 if not found"""
    for index, value in enumerate(lst):
        if value == val:
            return index
    return -1
```
- This approach looks at each name, one after the other, until I find the one I am looking for
- 
 It is also how the `lst.index(val)` method is implemented

# Can we do better?
- 
 No!
- 
 Linear search is optimal if the items are **unsorted**.
- 
 What if the items are **sorted**?

## An Idea: Using Sortedness
1. Look at a name in the middle of the phonebook
2. 
 If it is the name I am looking for, I'm done!
3. 
 If the name I want **comes after** the middle name
    - 
 Ignore the names to the left
    - 
 Goto step 1 to continue searching the right-half
4. 
 If the name I want  **comes before** the middle name
    - 
 Ignore the names to the right
    - 
 Goto step 1 to continue searching the left-half

# Binary Search

## Binary Search Pseudocode
```py[1-7|8|9-10|11-12|13-14|1-14]
def binary_search(val, lst):
    """Finds the index of val in lst or -1 if not found

Preconditions:
        lst is sorted using < (ascending order)
        val < x is defined for each x in lst
    """
    # mid = the middle element of lst
    # if mid == val, then
    #     return the index of mid
    # else if mid < val, then
    #     continue searching the right half
    # else
    #     continue searching the left half
```

## Binary Search Pseudocode
- How will we keep track of the part of the `lst` that still needs to be searched?
- 
 **Idea:** have `low` and `high` variables that keeps track of the range of indices

![animation of binary search](/teaching/2021s/cs65/assets/images/binary-search.gif)

**Credit:** www.mathwarehouse.com

## Binary Search Pseudocode
```py[1|2-3|4|5|6-7|8-9|10-11|13-14|1-14]
def binary_search(val, lst):
    # low = first index of lst
    # high = last index of lst
    # while there are still elements in low...high:
    #     mid = the middle index between low and high
    #     if val == lst[mid]:
    #         return mid
    #     elif lst[mid] < val:
    #         update low...high range to be right of mid
    #     else:
    #         update low...high range to be left of mid
    #
    # if we get here, there are no more elements to search
    # so we should return -1
```

## Binary Search Implementation
```py
def binary_search(val, lst):
    low = 0                      # first index
    high = len(lst) -1           # last index
    while low <= high:           # while at least one left
        mid = (high + low) // 2  # middle index
        if val == lst[mid]:      # if we found val
            return mid           #   return its index
        elif val > lst[mid]:     # if val is to the right
            low = mid + 1        #   search to the right
        else:                    # if val is to the left
            high = mid - 1       #   search to the left

return -1                    # no more elements
```

# Searching Comparison

## Searching Comparison
- We've seen two strategies for searching for a value within a list
    1. **Linear Search:** Looks at one element at a time until we find it
    2. **Binary Search:** If the list is sorted, we can "zooms in" on the location of the value much quicker
- 
 What do we mean by **quicker** though?
    + Is it twice as fast? Three times as fast?

## Searching Comparison
- One common way to compare the efficiency of searching algorithms is by comparing the **number of comparisons** each algorithm uses

![animation of binary search](/teaching/2021s/cs65/assets/images/binary-and-linear-search.gif)

## Searching Comparison
- What is the **worst case** number of comparisons required for each algorithm?
    + 
 For both algorithms, the worst case is when `lst` does not contain `val` so it has to do a lot of comparisons
- 
 Suppose that `len(lst) = 1024`
    + 
 **Linear**: 1024 comparisons in worst case
    + 
 **Binary**: 10 comparisons in worst case

## Searching Comparison
- Now suppose that `len(lst) = 2048`
    + 
 **Linear**: 2048 comparisons in worst case
    + 
 **Binary**: 11 comparisons in worst case
- 
 Finally, suppose that `len(lst) = $N$`
    + 
 **Linear**: `$N$` comparisons in worst case
    + 
 **Binary**: `$\log_2(N)$` comparisons in worst case

# Divide and Conquer Algorithms

## Divide and Conquer Algorithms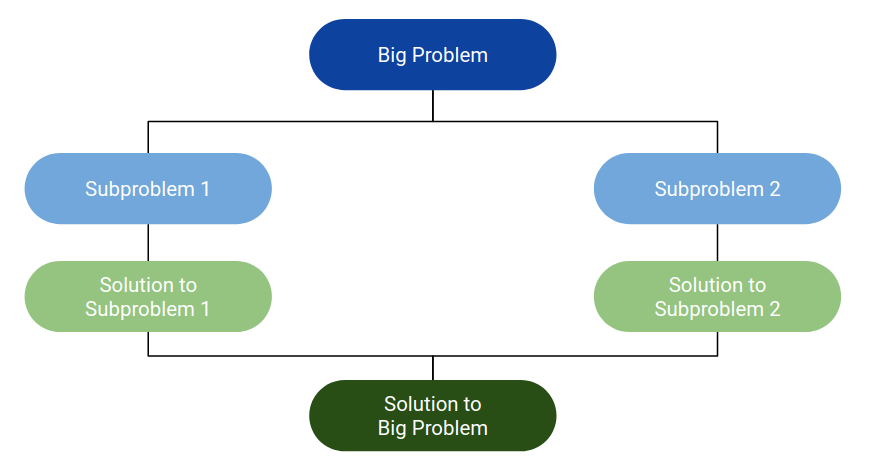

![split big problem into subproblems](/teaching/2021s/cs65/assets/images/divide-and-conquer.png)

## Divide and Conquer Algorithms
1. **Divide** big problem into smaller parts
2. **Solve** problems independently
3. **Combine** answers to yield solution to big problem

## Divide and Conquer Algorithms
- Suppose I’d like to write a function `sum(numbers)` that returns the **sum** of all the numbers in a list.
- 
 We could implement this with a loop, but let’s try a different approach!
- 
 Given list: `numbers = [5, 7, 3, 2, 9, 4]`
- 
 How can we **divide** the list into easier subproblems?
    + 
 `sum([5, 7, 3]) + sum([2, 9, 4])`
    + 
 `5 + sum([7, 3, 2, 9, 4])`

# Recursion

## Recursion
- A **recursive** function is one that "refers to itself"
- 
 In mathematics, recursive functions are used regularly
- 
 You might recall the **factorial** function: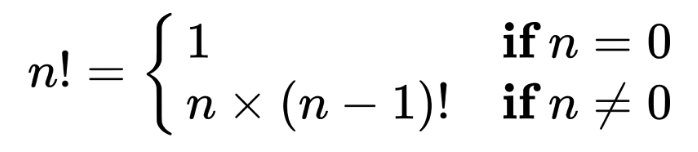

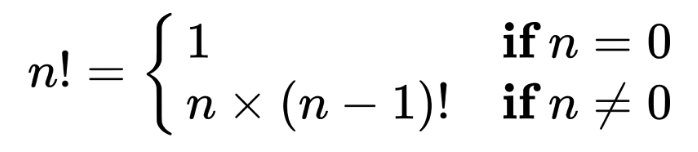![factorial function definition](/teaching/2021s/cs65/assets/images/factorial.png)

## Recursion
![factorial function definition](/teaching/2021s/cs65/assets/images/factorial.png)

- Python supports implementing functions recursively

```py
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)
```

## Recursion: Two Basic Parts
- **Base Case**:
    + 
 The “when to stop” case of recursion
    + 
 (Usually the simplest conceivable subproblem)
- 
 **Recursive Case**:
    + 
 Break the problem into smaller subproblems
    + 
 (Each subproblem should get "closer" to a base case)
    + 
 Solve the subproblems by making recursive calls
    + 
 Combine results into the answer

## Adding Recursively
- Recall that we can **divide** `[5, 7, 3, 2, 9, 4]` into smaller problems:
    + `sum([5, 7, 3]) + sum([2, 9, 4])`
- What goes in the ???s to complete the algorithm?

---

```py
def sum(numbers):
    if ???:                       # Base case
        return ???
    else:
        mid = len(numbers) // 2   # Recursive case
        return ???
```

## Adding Recursively
```py
def sum(numbers):
    if len(numbers) == 0:
        return 0
    else:
        mid = len(numbers) // 2
        return sum(numbers[:mid]) + sum(numbers[mid:])
```

```py
def sum(numbers):
    if len(numbers) == 0:
        return 0
    else:
        return numbers[0] + sum(numbers[1:])
```

# Other Examples

## Reversing a String
- Suppose we want to write the function `reverse(s)` that takes a string and returns the **reversed** version of `s`
    + `reverse("abc")` should return `"cba"`
- 
 How can we do this recursively?

## Reversing a String
- We need to think about two things:
    + 
 How can we **break up** the problem into one or more simpler subproblems?
    + 
 What is the **simplest** conceivable subproblem?

## Reversing a String
- **Observation**: these should be the same:
    + `reverse("abcdef")`
    + `reverse("bcdef") + "a"`
- 
 The **subproblem** that is easier than the original
    + 
 Uses the fact that concatenating two strings is easy
    + 
 If we have a solution to the subproblem, we can solve the bigger problem with a simple use of `+`

## Reversing a String

- Here is a partial solution so far:
```py
def reverse(s):
    """Reverses the string s"""
    return reverse(s[1:]) + s[0]
```
- 
 But we are missing the **base case**
- 
 What is the simplest conceivable subproblem?
    + 
 **Idea**: a single character (or the empty string)

## Reversing a String
```py
def reverse(s):
    """Reverses the string s"""
    if len(s) <= 1:    # if s is "a"
        return s       # then "a" is its own reverse
    else:
        # if s is "abc", solve it with reverse("bc") + "a"
        return reverse(s[1:]) + s[0]
```

## Repeated Concatenation
- Recall that `3*"ab"` in Python computes `"ababab"`
- 
 Suppose we want to write it as a function:
    + `string_star(num, s)`
    + 
 `string_star(3, "ab")` should be `"ababab"`
- 
 Two questions for you:
    + 
 What is the **simplest** form of the problem that we can immediately return the answer for?
    + 
 How can you **break up** the problem into one or more smaller subproblems?

## Repeated Concatenation
+ Use the fact that the following are the same:
    * `string_star(3, "ab")`
    * `"ab" + string_star(2, "ab")`
+ 
 Use `num == 1` as the base case

```py
def string_star(num, s):
    if num == 1:
        return s
    else:
        return s + string_star(num-1, s)
```