reveal.js

# Recursion, Continued

---

CS 65 // 2021-04-22

## Administrivia
- Project proposal due today
- 
 Check in

# Exam 3

## Exam 3
- Exam 3 is released
- Be sure to carefully read the [exam procedures]( ../../resources/exam-procedures.html) before starting the exam
- 
 It is an **individual**, take-home exam
    + 
 No discussing with peers, mentors, or tutors
    + 
 You may only discuss the exam with me

# Questions
## ...about anything?

# Divide and Conquer Algorithms

## Divide and Conquer Algorithms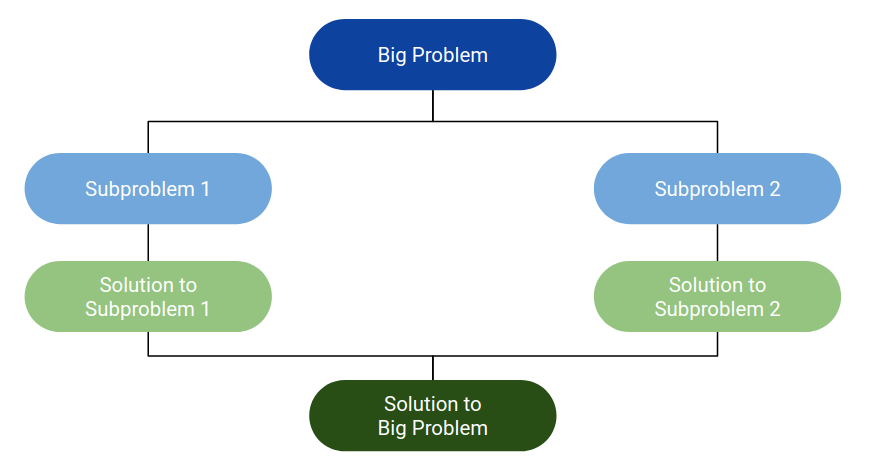

![split big problem into subproblems](/teaching/2021s/cs65/assets/images/divide-and-conquer.png)

## Divide and Conquer Algorithms
1. **Divide** big problem into smaller parts
2. **Solve** problems independently
3. **Combine** answers to yield solution to big problem

## Divide and Conquer Algorithms
- Suppose I’d like to write a function `sum(numbers)` that returns the **sum** of all the numbers in a list.
- `numbers = [5, 7, 3, 2, 9, 4]` can summed by:
    + 
 **Divide** into `[5, 7, 3]` and `[2, 9, 4]`
    + 
 **Solve** each problem independently
        * `sum([5, 7, 3]) ===> 15`
        * 
 `sum([2, 9, 4]) ===> 15`
    + 
 **Combine:** `15 + 15 ===> sum(numbers)`

# Recursion

## Recursion
- A **recursive** function is one that "refers to itself"
- 
 In mathematics, recursive functions are used regularly
- 
 You might recall the **factorial** function can be implemented with:

```py
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)
```

## Recursion: Two Basic Parts
- **Base Case**:
    + 
 The “when to stop” case of recursion
    + 
 (Usually the simplest conceivable subproblem)
- 
 **Recursive Case**:
    + 
 Break the problem into smaller subproblems
    + 
 (Each subproblem should get "closer" to a base case)
    + 
 Solve the subproblems by making recursive calls
    + 
 Combine results into the answer

## Adding Recursively
- Recall that we can **divide** `[5, 7, 3, 2, 9, 4]` into smaller problems:
    + `sum([5, 7, 3]) + sum([2, 9, 4])`
- What goes in the ???s to complete the algorithm?

---

```py
def sum(numbers):
    if ???:                       # Base case
        return ???
    else:
        mid = len(numbers) // 2   # Recursive case
        return ???
```

## Adding Recursively
```py
def sum(numbers):
    if len(numbers) == 0:
        return 0
    else:
        mid = len(numbers) // 2
        return sum(numbers[:mid]) + sum(numbers[mid:])
```

```py
def sum(numbers):
    if len(numbers) == 1:
        return numbers[0]
    else:
        return numbers[0] + sum(numbers[1:])
```

# Other Examples

## Reversing a String
- Suppose we want to write the function `reverse(s)` that takes a string and returns the **reversed** version of `s`
    + `reverse("abc")` should return `"cba"`
- 
 How can we do this recursively?

## Reversing a String
- We need to think about two things:
    + 
 How can we **break up** the problem into one or more simpler subproblems?
    + 
 What is the **simplest** conceivable subproblem?

## Reversing a String
- **Observation**: these should be the same:
    + `reverse("abcdef")`
    + `reverse("bcdef") + "a"`
- 
 The **subproblem** `"bcdef"` is smaller
    + 
 Uses fact that concatenating two strings is easy
    + 
 If we have a solution to the subproblem, we can solve the bigger problem with a simple use of `+`
- 
 Can we generalize this idea to an arbitrary string `s`?
    + How can we simplify `reverse(s)`?

## Reversing a String
- Here is a partial solution so far:
```py
def reverse(s):
    """Reverses the string s"""
    return reverse(s[1:]) + s[0]
```
- 
 But we are missing the **base case**
- 
 What is the simplest conceivable subproblem?
    + 
 **Idea**: a single character (or the empty string)

## Reversing a String
```py
def reverse(s):
    """Reverses the string s"""
    if len(s) <= 1:    # if s is "a"
        return s       # then "a" is its own reverse
    else:
        # if s is "abc", solve it with reverse("bc") + "a"
        return reverse(s[1:]) + s[0]
```

## Repeated Concatenation
- Recall that `3*"ab"` in Python computes `"ababab"`
- 
 Suppose we want to write it as a function:
    + `string_star(num, s)`
    + 
 `string_star(3, "ab")` ==> `"ababab"`
- 
 **Think** about the following questions:
    + 
 What is the **simplest** form of the problem that we can immediately return the answer for?
    + 
 How can you **break up** the problem into one or more smaller subproblems?

## Repeated Concatenation
+ Use the fact that the following are the same:
    * `string_star(3, "ab")`
    * `string_star(2, "ab") + "ab"`
+ 
 Use `num == 1` as the base case

```py
def string_star(num, s):
    if num == 1:
        return s
    else:
        return string_star(num-1, s) + s
```

# Binary Search Revisited

## Binary Search Pseudocode

```py
def binary_search(val, lst):
    """Returns the index of val in lst or -1 if not present

Preconditions:
        * lst is sorted using < (ascending order)
        * val < x is defined (for each x in lst)
    """
    # mid = the middle element of lst
    # if mid == val, then
    #     return the index of mid
    # else if val < mid, then
    #     continue searching the left half
    # else
    #     continue searching the right half
```

## Recursive Binary Search
```py
def binary_search(val, lst):
    mid = len(lst) // 2 
    if len(lst) == 0:         # base case
        return -1
    elif lst[mid] == val:
        return mid
    elif val < lst[mid]:
        return binary_search(val, lst[:mid])
    else:
        return (mid+1) + binary_search(val, lst[mid+1:])
```

## Recursive Binary Search
- The previous recursive solution works great, but slicing a list is a slow operation
- Let's try another approach that avoids slicing
- 
 We can use a **helper function** to keep track of the `low` and `high` variables
```py
def binary_search_range(val, lst, low, high):
    """Returns the index of val in lst,
    searching only the range between low...high"""
```
- 
 Then `binary_search` can be implemented with
```py
def binary_search(val, lst):
    return binary_search_range(val, lst, 0, len(lst)-1)
```

## Recursive Binary Search
```py
def binary_search_range(val, lst, low, high):
    """Returns the index of val in lst,
    searching only the range between low...high"""
    mid = (low + high) // 2
    if low > high:
        return -1
    elif lst[mid] == val:
        return mid
    elif val < lst[mid]:
        return binary_search_range(val, lst, low, mid-1)
    else:
        return binary_search_range(val, lst, mid+1, high)
```

# Other Cool Examples